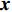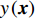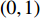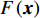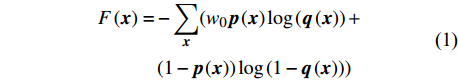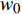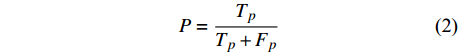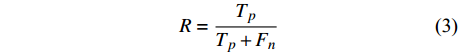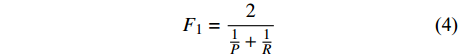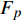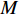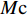Automatic Seismic Phase Picking Method APP++ based on Deep Learning and Array Strategy and Its Application in Sichuan-Yunnan Region
-
摘要: 在APP方法的基础上，使用U-net++模型，提出了进一步的改进算法APP++用于台阵下的震相到时自动拾取，测试结果显示，APP++模型在具有和APP相当的拾取能力的同时，还能够更好地避免误识别，且具有跨区域泛化能力；将该方法用于川滇地区的固定台网和流动台阵上，扫描了2014—2019年6年的连续数据，检测到了73 291条地震，发现很好地符合G-R关系，完备震级在1/5～2级之间；地震的空间分布和该区域的断层有很好的一致性；由此计算得到的b值分布图也显示出和当地断层形态、应力状况很好的一致性，研究结果很好地展示了APP++方法的实用性。Abstract: On the basis of APP method, a further improved algorithm, APP++, is proposed by using U-Net ++ model, which is used to automatically pick up seismic phase on time under the array. The test results show that APP++ model has the same picking ability as APP, but also can avoid misidentification better, and has the ability of cross-region generalization. The method was applied to the fixed seismic network and mobile seismic array in Sichuan-Yunnan region, and the continuous data from 2014 to 2019 were scanned. 73 291 earthquakes were detected, which fit the G-R relationship well, and the complete magnitude was in the range of 1/5～2. The spatial distribution of earthquakes is in good agreement with the faults in this region. The calculated B-value distribution map also shows good agreement with the local fault morphology and stress state. The result show the practicability of APP++ method very well.
-
0 引言
近年来，深度学习方法在地震学领域的广泛应用，如地震检测与震相拾取[1-4]、信号的插值与降噪[5-6]、地下结构反演[7]等方面取得了很好的结果。特别是在地震检测与震相拾取方面，基于深度学习的方法已经能够达到甚至超过人工拾取的精度，而且在一致性、效率等方面有显著优势。在图像识别领域发展起来的U-net[8]深度学习网络是目前深度学习震相拾取方法效果最好的网络结构之一[1, 3-4]，其收缩路径允许网络提取更多、更复杂的特征，提高分类的准确率，带直连的扩展路径则有助于网络对检测目标进行更精确的定位。同时U-net网络模型具有良好的泛化能力，使得在一个区域训练得到的震相拾取模型在另一个区域也可以获得较好的效果[4]，极大地降低了该方法的迁移成本。U-net++[9]是在U-net基础上发展起来的网络结构，包括了多重收缩和扩展路径，使得网络具有更高的连接密度，能够更好地学习不同尺度的特征，以对不同尺度的对象进行检测。本文在刘芳等[4]设计的PP模型基础上，使用U-net++改进原有网络结构，提出了APP++震相拾取模型，达到了更好的单台地震体波震相检测水平。
尽管使用单台波形检测的准确率已经达到很高水平，但由于局部噪声的影响，会产生很多误识别结果。将高精度的单台检测和台阵策略相结合，则可以有效地降低误识别的比例[4, 10]，使得自动拾取算法应用在实际数据中具有实用性。刘芳等[4]将蒋一然等[10]提出的台阵策略与深度学习震相拾取模型结合，提出了APP方法。本文进一步将PP++单台震相拾取方法与台阵策略结合起来，并提出了适用于台阵数据的地震检测与震相拾取方法APP++。
最后，将APP++方法运用到川滇地区的固定台网和流动台阵中，检测了该区域2014—2019年间的地震并拾取了其体波到时。拾取结果显示，在川滇地区地震空间分布和断层有明显的相关性。
1 APP++震相拾取方法
1.1 PP++深度学习震相的拾取模型
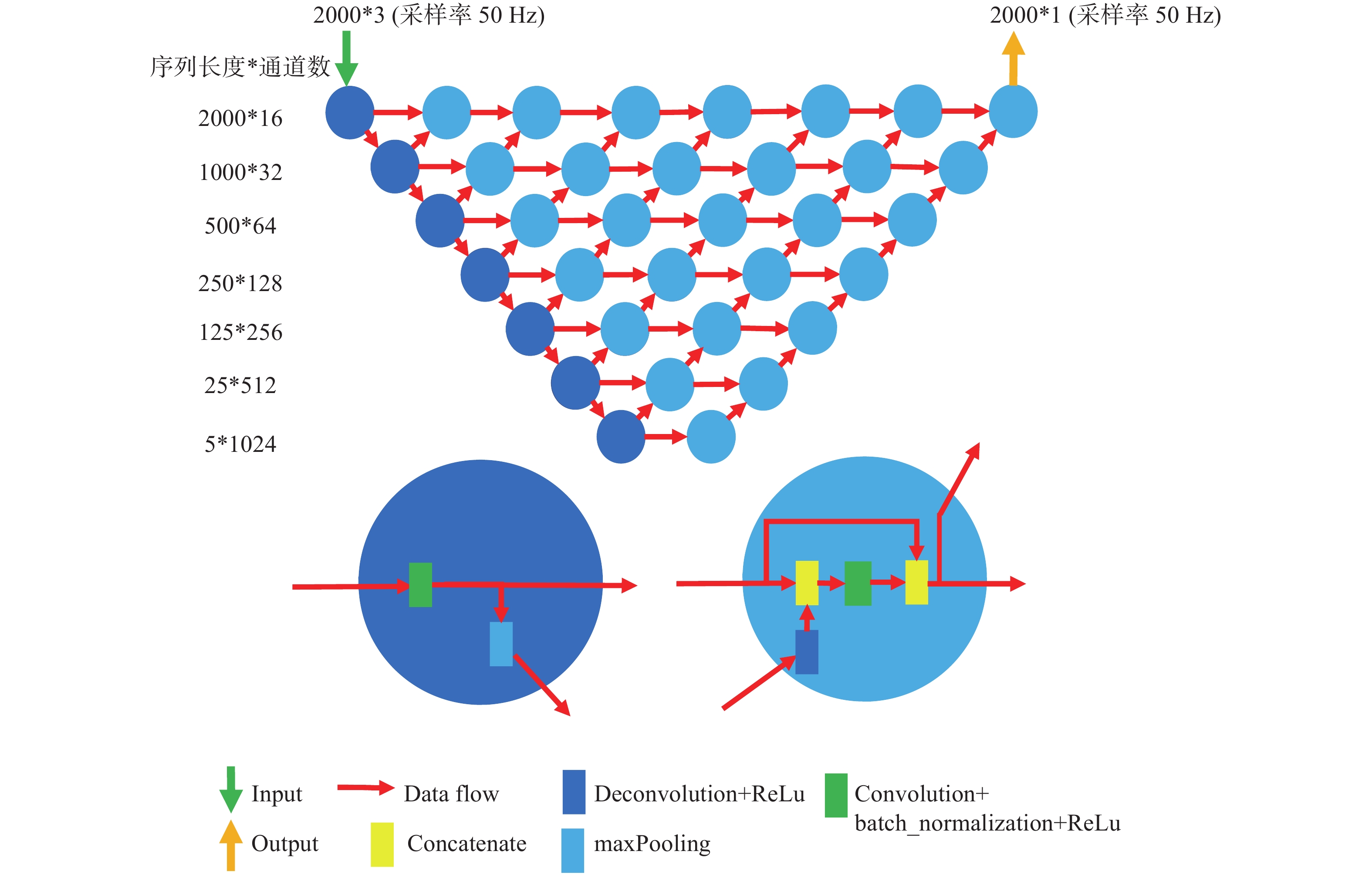
U-net++[9]是在U-net基础上发展起来的一种密接神经网络模型，在相同深度的情况下，U-net++具有更高的连接密度，能够提取更多尺度的特征，在部分图像识别任务上表现出更强的性能。设计的模型网络结构如图1所示，以40 s长度波形、50 Hz采样率的三分量波形为输入，通过7层的网络结构，输出与输入波形具有相同长度、从一个通道输出的预测结果。模型具有多个层次的扩展路径，在一个扩展路径单元，对更深层单元的输入进行反卷积和激活，并将结果和同一层中前一个单元的输出拼接起来作为该单元的输出。这样设计的网络中，较浅层次的网络获取较小尺度范围内的特征；较深层次的扩展网络收缩路径，把较浅层次的扩展网络的输出作为输入，可以更加综合地获取对象的不同尺度图像，提高网络判断的准确率和精确度。
![]()
图 1 PP++震相拾取模型注：深蓝色单元为收缩单元，包括卷积层、池化层、激活层和批量归一化层；浅蓝色为扩展单元，包括反卷积层、池化层、激活层、批量归一化层和拼接层。扩展单元中，反卷积以更深层单元的输出作为输入，并把反卷积经过激活、批量归一化后的结果和同层左侧相邻单元的输出拼接作为整个单元的输出。U-net++是在医学图像识别领域发展起来的，识别的对象相对于整个图像而言只占一小部分，使得较浅层次的模型也能在小尺度上对对象进行识别。因此，U-net++可以在多个扩展路径上都输出判别结果，用于优化参数。这样，使得具体的几个层次的输出都能拟合上目标输出，从而增加了模型的约束，避免模型过拟合。考虑到震相拾取问题需要根据地震波到达之前的噪声水平、整段波形的偏振变化等信息才能做出准确判断，涉及到的尺度和整个时间窗相当，浅层路径无法有效提取这些信息[4]，所以只关注最深层次的拓展路径输出结果，而不对其他浅层输出结果做约束。
相比于使用一个模型同时拾取P波和S波，使用相同网络结构、但参数不同的两个模型分别拾取P波和S波时可以避免不同震相拾取结果间的相互干扰，从而获得更高的拾取准确率和精确度[4]。基于这种考虑，PP++模型直接输出的时间序列
$ {{y}}\left({{x}}\right) $ 只有一个通道，大于0表示属于P波（S波），否则为噪声或其他震相，这里$ {{x}} $ 表示作为模型输入的波形三分量。在直接输出后加入Sigmoid函激活层，将直接输出$ y\left({{x}}\right) $ 映射到$ \left({0,1}\right) $ 之间，表示对象为P波（S波）概率$ {{q}}\left({{x}}\right) $ 的大小[4, 11]，大于0.5则视为P波（S波），否则视为噪声或其他震相。和PhaseNet、APP等U-net型震相拾取方法类似[1, 4]，将震相到时转换为高斯概率分布形式的时间序列
$ {{p}}\left({{x}}\right) $ ，震相到时作为高斯分布的中心（图2～3）。高斯概率函数的形态应与震相拾取的精度匹配，这里使用了高精度的样本集Hi-net和STEAD[12–14]，因此设置P波和S波的高斯函数标准差分别为0.08 s和0.12 s。为了保证样本集中震相部分和噪声部分的均衡，设置和刘芳等[4]相同的带权重的交叉熵损失函数
$ F\left({{x}}\right) $ $$\begin{aligned} F\left({{x}}\right)=&-\sum\limits_{{{x}}}({w}_{0}{{p}}\left({{x}}\right)\mathrm{log}\left({{q}}\left({{x}}\right)\right)+\\ &\left(1-{{p}}\left({{x}}\right)\right)\mathrm{log}\left(1-{{q}}\left({{x}}\right)\right))\end{aligned} $$ (1) 经过试验，设置
$ {w}_{0} $ 为24。使用Hi-net台网的目录、波形数据和STEAD地震波形、到时数据集共118万条作为训练的样本集。为尽可能地模拟对连续波形进行扫描的情形，对于样本集中波形随机选取时间窗，使得震相随机地分布于选取的时间窗内（图2～3）。
1.2 PP++模型的训练和测试
选取样本集中的1 104 914条记录作为训练集，30 000条样本作为验证集，50 000条样本作为测试集。训练过程中，每轮在训练集中随机选取5 000条样本，并根据损失函数使用验证集对每轮生成的模型进行评估；当模型在验证集上的损失函数超过50轮迭代后仍然没有降低时，则停止迭代，选取损失函数最小的模型作为最终的模型；利用最终得到的模型在测试集上进行评价。
评价标准首先包括Zhu等[1]和刘芳等[4]使用的评价参数：准确率（P）、召回率（R）、综合正确率（F1）、误差均值（mean）、误差均值（std）。准确率（P）、召回率（R）、综合正确率（F1）的表达式如下：
$$ P=\frac{{T}_{p}}{{T}_{p}+{F}_{p}} $$ (2) $$ R=\frac{{T}_{p}}{{T}_{p}+{F}_{n}} $$ (3) $$ {F}_{1}=\frac{2}{\frac{1}{P}+\frac{1}{R}} $$ (4) 式中：当模型预测概率>0.5、且与人工标注误差在0.5 s以内，视为正确的正预测，计入
$ {T}_{p} $ ；当模型预测概率>0.5、但与人工标注误差>0.5 s，视为错误的正预测，计入$ {F}_{p} $ ；当模型预测概率始终<0.5、但该段时间内确有人工标注震相时，视为错误的负预测，计入$ {F}_{n} $ ；$ F $ 表示准确率和召回率的调和平均。具体地讲，准确率反映的是，当模型给出正预测时正确拾取震相的比例；召回率反映的是，对于人工标注的震相，模型能够准确拾取的比例。一般来讲，设置高的标准，可以获得更好的准确率，但是召回率会下降；设置低的标准，则会提高召回率，但准确率下降。故需要将两者结合起来看，才能够更为合理地评价模型。较为通常的做法就是引入一个综合正确率，即对准确率和召回率取调和平均。同时，还需要衡量模型在连续数据上误识别比例的高低。震相拾取方法的应用场景中最为困难的是对连续数据的扫描。在实际数据中存在很多局部噪声，而且仪器异常干扰也会引起仪器的误识别。另外，在实际波形资料中，大部分时间的记录是不存在震相的噪声，即使模型对于噪声只有很低的误识别率，也容易产生大量的误识别结果。需要通过大量的噪声数据来对模型进行测试，从而衡量模型的抗干扰能力。如果在直接被人工标注过震相的连续数据中把未有人工标注的片段作为噪声数据，则其中会遗漏很多小能量的震相，从而无法反映真实的误识别比例。即使人工检视过的噪声资料也存在同样的问题，未看到明显震相的记录中可能也包含被噪声能量掩盖的小能量震相，而APP++震相拾取模型在这个时候则能体现其优越性。本文采取人工生成的方式，来避免缺乏噪声测试样本的问题。随机生成标准差为1的三分量连续波形共100天，每天的连续波形中随机在一些时间点加入300个大幅值的突变。使用模型扫描生成的数据，统计输出大于0.5的次数作为误识别次数，并计算平均每天误识别的次数，记为
$ M $ （单位为count per day，CPD）。当然，人工生成的噪声数据的分布和实际记录不完全一致，所以与在实际数据中的误识别比例会存在差异。因此，主要的关注点为将不同模型在人工噪声上误识别比例的相对大小用于评价不同模型的抗干扰能力的相对高低。由于Hi-net和STEAD两个样本集来自不同的地区，故分开统计两个测试集。为比较PP++模型与PP模型的效果差异，同时也采用相同的设置对PP模型进行测试。值得注意的是，PP++模型具有更高的连接密度，在同样尺寸设置下会比PP模型拥有更多的训练参数。为避免训练参数的数量影响对网络结构的评价，增加了PP模型的规模（74 720 001个参数），使得其与PP++模型（77 885 201个参数）相当。
表1是两个模型的测试结果。PP++和PP在前五项指标上差别不大，主要的差别体现在第六项日均误识别次数。在使用两个数据集一起训练的时候，识别P波的PP模型与识别P波和S波的PP++模型的日均误识别次数都在一次以内，而对于识别S波的PP模型则达到了15。由此表明，使用U-net模型训练的S波拾取模型可能在数据质量较差的时候受到很强的干扰从而产生较多的误识别比例。而U-net++则可以较好地避免这种情况，即PP++模型相对于PP模型更有优势。比较两个数据集的测试结果，尤其是对S波的拾取上，STEAD样本集上效果在大多数时候更好，可能是因为STEAD样本集中的样本震中距更小，震相更为简单。
表 1 PP++和PP模型测试结果震相 模型 训练与验证集 测试集 Hi-net STEAD Synthetic P R F1 mean/s std/s P R F1 mean/s std/s M（CPD） P波 PP++ All 0.977 0.975 0.976 0.011 0.080 0.987 0.986 0.986 0.002 0.081 0.36 Hi-net 0.977 0.974 0.976 0.007 0.078 0.969 0.922 0.945 −0.049 0.109 7.98 PP All 0.977 0.975 0.976 0.006 0.079 0.987 0.987 0.987 0.003 0.080 0.19 Hi-net 0.978 0.976 0.977 0.009 0.078 0.967 0.916 0.941 −0.048 0.114 30.32 S波 PP++ All 0.922 0.920 0.921 0.010 0.129 0.963 0.963 0.963 −0.001 0.121 0.83 Hi-net 0.923 0.921 0.922 0.001 0.127 0.948 0.930 0.939 −0.040 0.125 1.51 PP All 0.924 0.922 0.923 0.016 0.128 0.963 0.963 0.963 0.003 0.121 15 Hi-net 0.927 0.925 0.926 0.003 0.127 0.954 0.936 0.945 −0.042 0.125 2.590 图4展示的是PP++模型拾取震相到时的误差分布。P波和S波在两个样本集的误差都很小，而且具有很好的对称性，反映出PP++模型具有很好的拾取效果。
1.3 APP++模型的泛化能力
高质量的样本集往往来自运行时间较长、数据处理流程成熟的固定台网。这类固定台网多数积累了大量的地震目录和震相到时数据，对于自动拾取算法的需求反而不迫切。而缺乏样本积累的新建固定台网和流动台网则比较迫切地需要高质量的自动拾取。如果使用一个台网的高质量样本集试验出来的模型能够在缺乏样本集积累的台网数据上应用，则可以很好地解决这个问题，同时也可以减少迁移到新数据上使用的成本，这就要求模型具有一定的泛化能力。U-net[8]这类端对端的深度学习模型，就具有较强的泛化能力，不容易发生过拟合。刘芳等[4]的研究也表明，U-net类的震相模型具有一定的跨区泛化能力，且使用具有较好拾取质量的异地样本集甚至可以获得比使用稍低质量的本地样本集更好的拾取效果。本文所使用样本的Hi-net主要来自日本及其周边区域的台站，而STEAD包含的台站基本覆盖了全球大部分区域。为了验证模型的泛化能力，使用Hi-net训练和验证模型，并使用STEAD对模型的效果进行测试（表1）。结果显示，PP模型和PP++模型具有良好的泛化能力，仅使用日本周边地区的地震进行训练也能在全球化的STEAD样本集中显示出很好的拾取效果。单独使用Hi-net样本集训练的时候，识别P波的PP模型、识别P波的PP++模型和识别S波的PP++模型，日均误识别率都显著提高。识别P波的PP++模型的日均误识别率低于识别P波的PP模型，识别S波的PP模型，日均误识别率有所下降，但仍高于同等情况下识别S波的PP++模型。总体上看，在使用小规模样本集的情况下，PP++模型的误识别率更低。识别S波的PP模型在小样本集上误识别率的下降也说明，PP模型的误识别率可能受样本集影响很大，不够稳定。因此，PP++模型在扫描连续数据时将具有更好的可靠性。
1.4 APP++模型：PP++与台阵策略结合
尽管单台的拾取精度已经很好，但是在扫描长时间的记录波形数据时，仍然会出现部分误识别。将单台的拾取方法和台阵策略结合，利用多台拾取结果间的时空关系，可以排除大多数局部噪音造成的误识别[10]。本文采用和刘芳等[4]相同的方法，将PP++模型与蒋一然等[10]的台阵策略结合，形成了台阵下的震相拾取方法APP++。
2 在川滇地区的应用
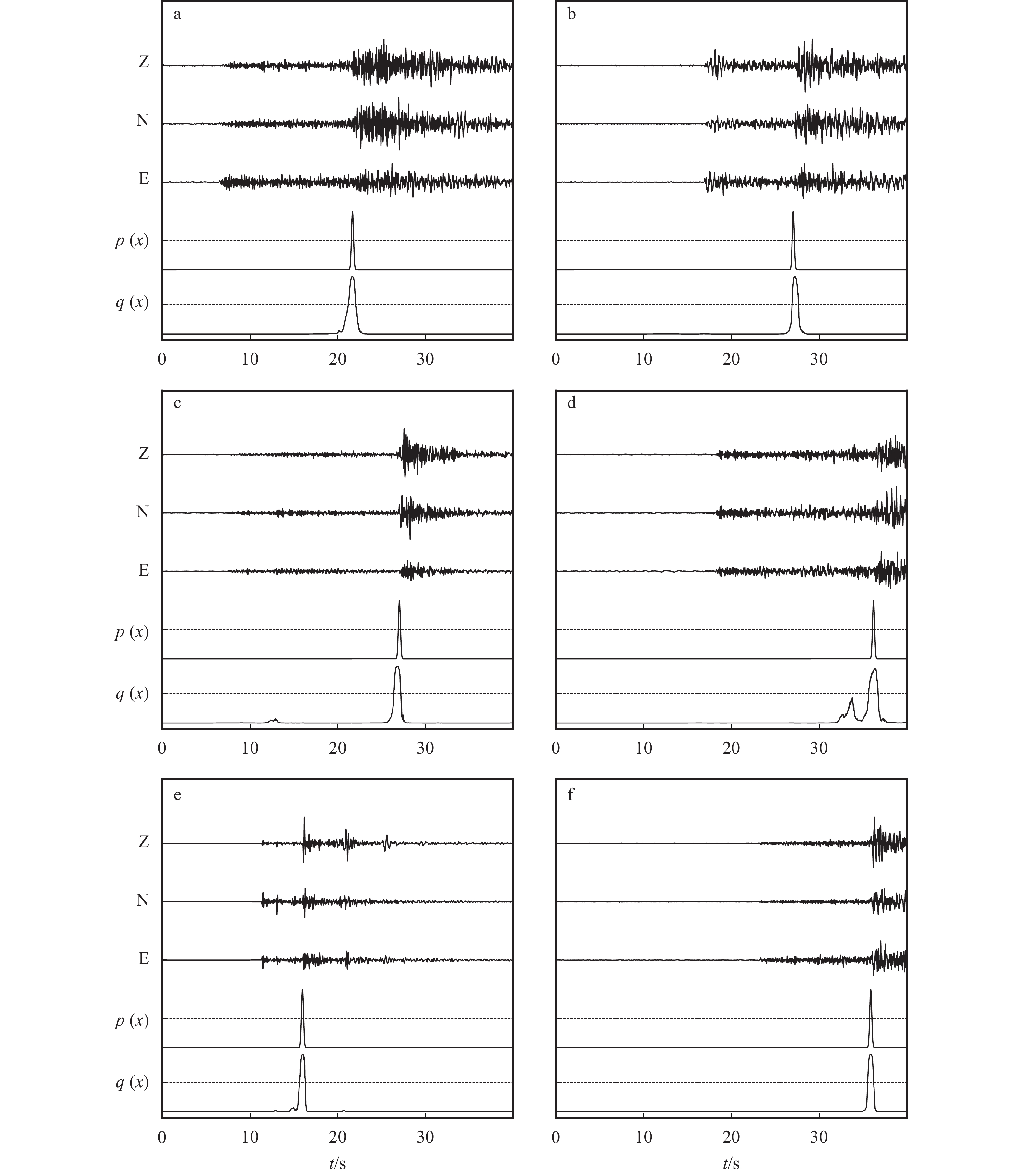
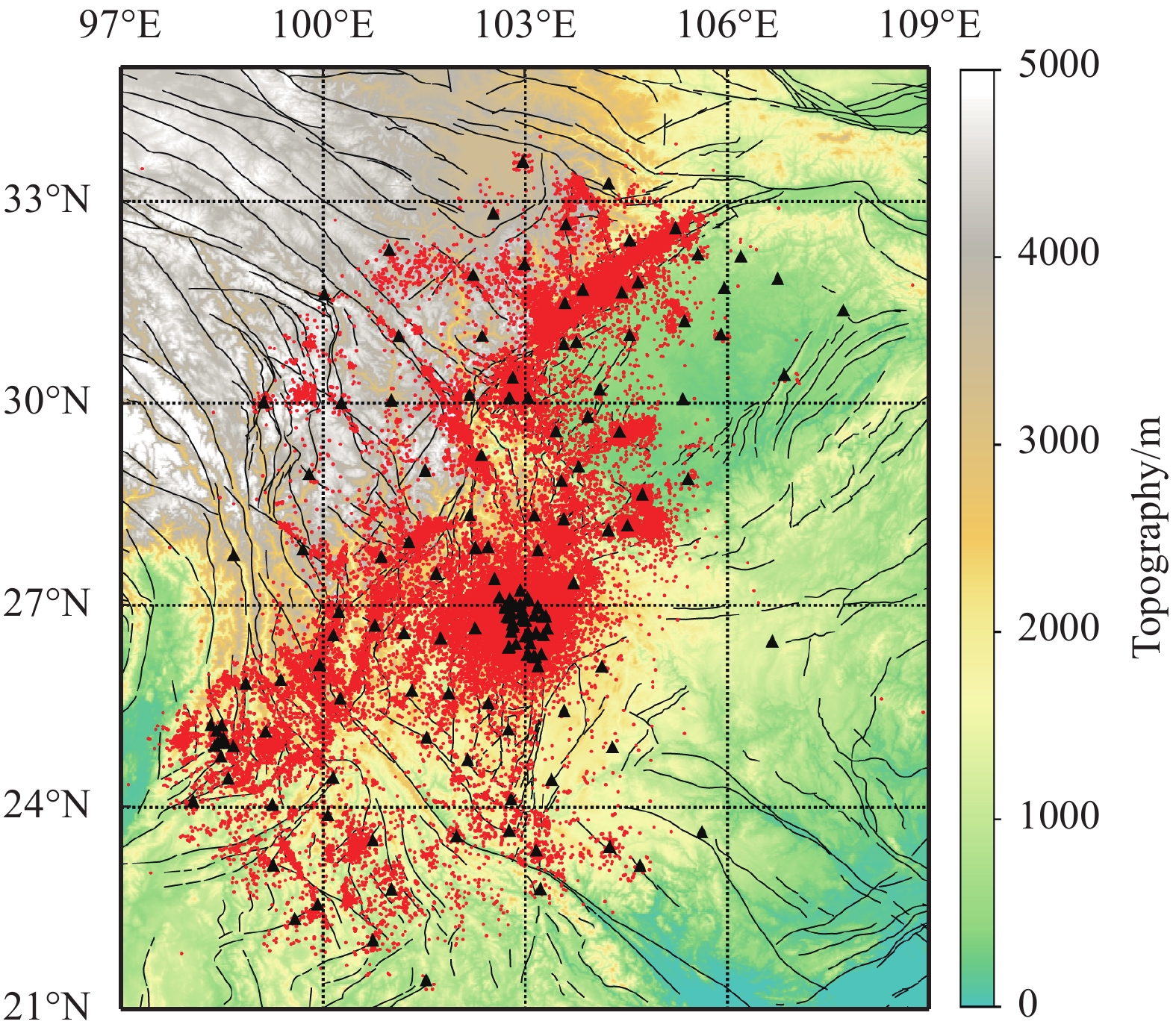
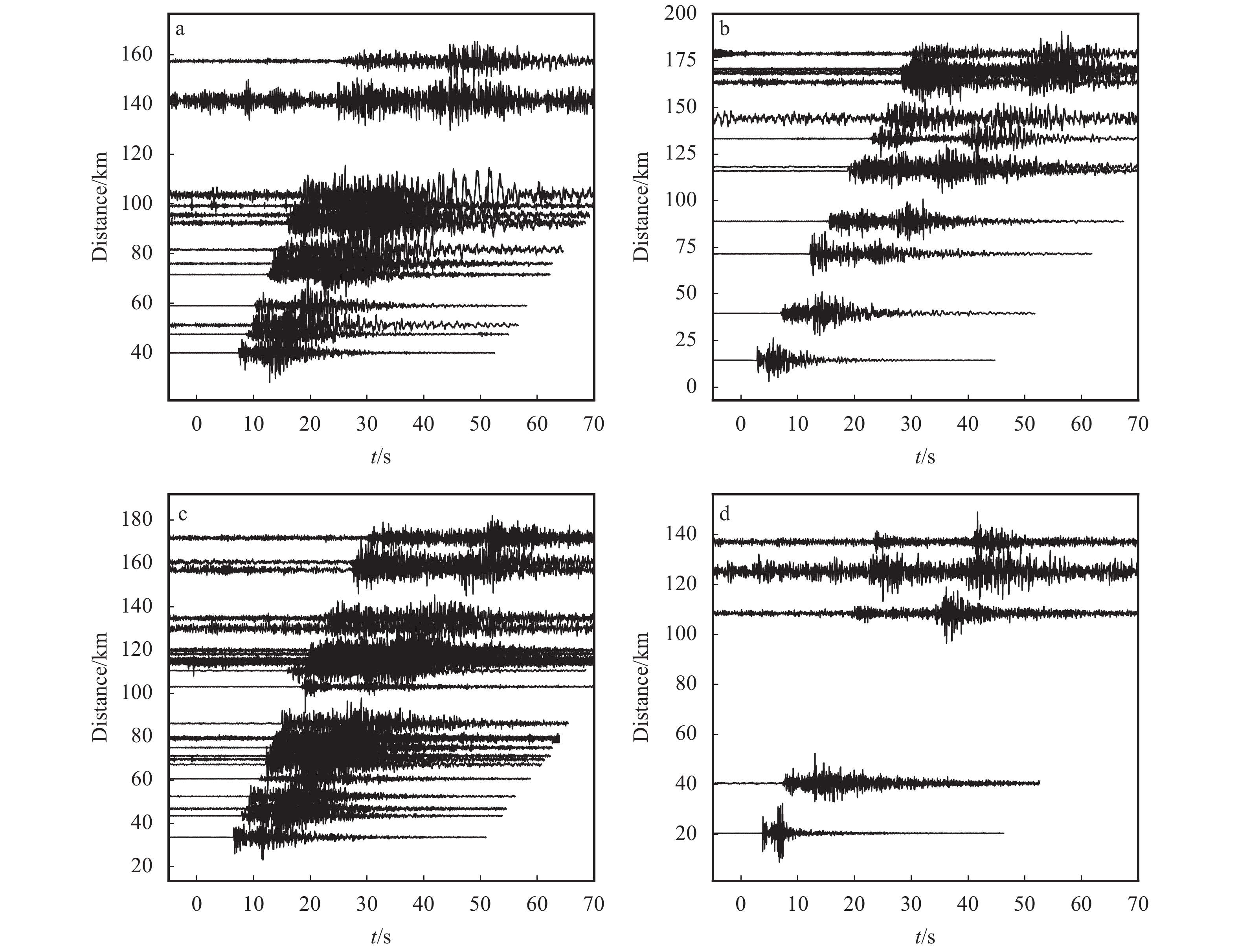
川滇地区位于青藏高原东南缘，构造运动活跃，是研究青藏高原隆起相关的物质运移等问题的重要研究场所，同时该地区具有很强的地震活动性，对该区域的研究有助于推进地震预测和预警研究的发展。因此，将使用Hi-net和STEAD样本集得到PP++模型和APP++方法应用到川滇地区的固定台网和流动台阵中的167个台站（位置移动过的台站视为不同台站）上。通过扫描2014—2019年共6年的连续波形，找到73 291个地震、537 554个P波记录、471 459个S波记录（图5）。图6是APP++方法拾取到的4个地震事件波形随震中距的分布及拾取到的震相到时，拾取结果和实际波形吻合较好，表明该方法能够用于对该区域地震的震相拾取。
3 拾取结果分析
图5展示的地震分布和当地的断层分布对应较好，后续研究中对这些地震进行精定位将有助于细致刻画该区域的断层结构。受台站分布密度的影响，在台站密集的区域，检测到地震多一些，台站稀疏的区域则检测到的地震相对较少。
图7a是地震数目的平均日变化（UTC+8）。图中显示，在夜间、中午、傍晚时间记录到的地震数目明显更多，这可能是因为在这些时间段正好是睡觉、吃饭的时间段，人类活动较少，环境噪声水平降低，同等台阵密度下记录到的地震变多。图7b是不同震级的累计地震数量分布图，符合G-R关系[15]，相应的完备震级应在1.5～2.0级之间。由于研究使用台阵的台间距在40 km左右，以单台判断为主的深度学习方法受信噪比限制无法再对更低的震级进行完备的检测，如使用弱模板识别[16]等方法则有可能进一步提高地震检测能力。
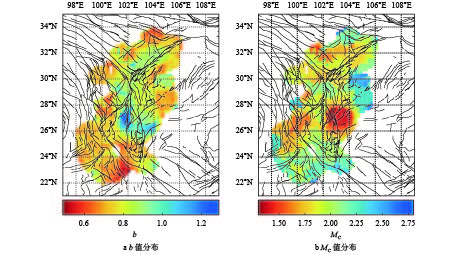
发震频率随震级变化的趋势可以用b值来描述，是研究地震活动性的重要指标。前人的研究结果表明，b值与当地的岩石状态、断层形态等相关[17-19]。本文采用MAXC[20-21]方法对研究区域内的b值和完备震级
$ M\mathrm{c} $ 进行了估计（中心点附近120 km，至少包含180个地震记录）（图8）。在龙门山断裂带上b值较附近区域偏低，但对于整个研究区域而言处于平均水平，这与前人的研究较为一致[22-23]。研究区域的北部和南部的低b值可能反映该地区较高的应力水平，而东部的低b值则与该地区的页岩气开采有关。完备震级（图8b）的空间分布和台站密度有很好的一致性，在被高密度的流动台网加密的小江断裂带附近，完备震级达到了1.5级以下。4 结论
1）在APP方法的基础上，利用U-net++改进了原有的深度学习网络，能够更好地避免噪声的干扰，并在测试中显示出一定程度的跨区域泛化能力。
2）进一步将海量数据训练得到的网络用于对川滇地区地震的扫描，检测出了大量的地震并拾取了其体波到时。分析发现：①拾取到的地震的空间分布和当地的断层有很好的一致性；②检测地震数量随时间的日变化反映了当地噪音水平对地震检测能力的影响；③地震发震频率随震级的变化满足G-R关系。
3）对研究区域内不同地点的b值做出了估计，b值的变化能够大致反映对应区域的应力状态变化情况。
致谢 中国地震局地震预测研究所为本研究提供地震波形数据；本研究工作得到北京大学高性能计算校级公共平台支持。
-
![]()
图 1 PP++震相拾取模型
注：深蓝色单元为收缩单元，包括卷积层、池化层、激活层和批量归一化层；浅蓝色为扩展单元，包括反卷积层、池化层、激活层、批量归一化层和拼接层。扩展单元中，反卷积以更深层单元的输出作为输入，并把反卷积经过激活、批量归一化后的结果和同层左侧相邻单元的输出拼接作为整个单元的输出。
表 1 PP++和PP模型测试结果
震相 模型 训练与验证集 测试集 Hi-net STEAD Synthetic P R F1 mean/s std/s P R F1 mean/s std/s M（CPD） P波 PP++ All 0.977 0.975 0.976 0.011 0.080 0.987 0.986 0.986 0.002 0.081 0.36 Hi-net 0.977 0.974 0.976 0.007 0.078 0.969 0.922 0.945 −0.049 0.109 7.98 PP All 0.977 0.975 0.976 0.006 0.079 0.987 0.987 0.987 0.003 0.080 0.19 Hi-net 0.978 0.976 0.977 0.009 0.078 0.967 0.916 0.941 −0.048 0.114 30.32 S波 PP++ All 0.922 0.920 0.921 0.010 0.129 0.963 0.963 0.963 −0.001 0.121 0.83 Hi-net 0.923 0.921 0.922 0.001 0.127 0.948 0.930 0.939 −0.040 0.125 1.51 PP All 0.924 0.922 0.923 0.016 0.128 0.963 0.963 0.963 0.003 0.121 15 Hi-net 0.927 0.925 0.926 0.003 0.127 0.954 0.936 0.945 −0.042 0.125 2.590 
下载: 导出CSV
-
[1] Zhu W Q, Beroza G C. PhaseNet: a deep-neural-network-based seismic arrival-time picking method[J]. Geophysical Journal International, 2019, 216(1): 261-273.
[2] Zhou Y J, Yue H, Kong Q K, et al. Hybrid event detection and phase‐picking algorithm using convolutional and recurrent neural networks[J]. Seismological Research Letters, 2019, 90(3): 1079-1087. doi: 10.1785/0220180319
[3] 赵明, 陈石, 房立华, 等. 基于U形卷积神经网络的震相识别与到时拾取方法研究[J]. 地球物理学报, 2019, 62(8): 3034-3042. doi: 10.6038/cjg2019M0495 [4] 刘芳, 蒋一然, 宁杰远, 等. 结合台阵策略的震相拾取深度学习方法[J]. 科学通报, 2020, 65(11): 1016-1026. [5] Jia Y N, Ma J W. What can machine learning do for seismic data processing? An interpolation application[J]. Geophysics, 2017, 82(3): V163-V177. doi: 10.1190/geo2016-0300.1
[6] Yu S W, Ma J W, Wang W L. Deep learning tutorial for denoising[EB/OL]. （2019-07-20）. https://arxiv.org/abs/1810.11614v1.
[7] Yang F S, Ma J W. Deep-learning inversion: a next-generation seismic velocity model building method[J]. Geophysics, 2019, 84(4): R583-R599. doi: 10.1190/geo2018-0249.1
[8] Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation[C]//International Conference on Medical image computing and computer-assisted intervention. Springer, 2015: 234-241.
[9] Zhou Z W, Rahman Siddiquee M, Tajbakhsh N, et al. UNet++: a nested u-net architecture for medical image segmentation[C]//4th International Workshop on Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support. Granada, Spain: Springer, 2018: 3-11.
[10] 蒋一然, 宁杰远. 基于支持向量机的地震体波震相自动识别及到时自动拾取[J]. 地球物理学报, 2019, 62(1): 361-373. doi: 10.6038/cjg2019M0442 [11] Little W A. The existence of persistent states in the brain[J]. Mathematical Biosciences, 1974, 19(1/2): 101-120.
[12] Obara K, Kasahara K, Hori S, et al. A densely distributed high-sensitivity seismograph network in japan: Hi-net by national research institute for earth science and disasterprevention[J]. Review of Scientific Instruments, 2005, 76(2): 021301. doi: 10.1063/1.1854197
[13] Okada Y, Kasahara K, Hori S, et al. Recent progress of seismic observation networks in Japan—Hi-net, F-net, K-NET and KiK-net—[J]. Earth, Planets and Space, 2004, 56(8): xv-xxviii. doi: 10.1186/BF03353076
[14] Mousavi S M, Sheng Y X, Zhu W Q, et al. STanford EArthquake dataset (STEAD): a global data set of seismic signals for AI[J]. IEEE Access, 2019, 7: 179464-179476. doi: 10.1109/ACCESS.2019.2947848
[15] Gutenberg B, Richter C F. Frequency of earthquakes in California[J]. Bulletin of the Seismological Society of America, 1944, 34(4): 185-188.
[16] 吴梦羽, 毛淑娟, 宁杰远, 等. 基于模板识别方法探测断层结构[J]. 北京大学学报: 自然科学版, 2018, 54(4): 730-738. [17] Scholz C H. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes[J]. Bulletin of the Seismological Society of America, 1968, 58(1): 399-415.
[18] Schorlemmer D, Wiemer S, Wyss M. Variations in earthquake-size distribution across different stress regimes[J]. Nature, 2005, 437(7058): 539-542. doi: 10.1038/nature04094
[19] Gulia L, Wiemer S. The influence of tectonic regimes on the earthquake size distribution: A case study for Italy[J]. Geophysical Research Letters, 2010, 37(10): L10305.
[20] Wiemer S, Wyss M. Minimum magnitude of completeness in earthquake catalogs: Examples from Alaska, the western United States, and Japan[J]. Bulletin of the Seismological Society of America, 2000, 90(4): 859-869. doi: 10.1785/0119990114
[21] Zhou Y J, Zhou S Y, Zhuang J C. A test on methods for MC estimation based on earthquake catalog[J]. Earth and Planetary Physics, 2018, 2(2): 150-162. doi: 10.26464/epp2018015
[22] 王辉, 曹建玲, 荆燕, 等. 川滇地区强震活动前b值的时空分布特征[C]//中国地球物理学会第二十八届年会论文集. 北京: 中国科学技术大学出版社, 2012: 241. [23] Zhang S J, Zhou S Y. Spatial and temporal variation of b-values in southwest China[J]. Pure and Applied Geophysics, 2016, 173(1): 85-96. doi: 10.1007/s00024-015-1044-7
-
期刊类型引用(3)
1. 蒋一然，宁杰远，李春来. GPU并行加速下的弱模板匹配及其在川滇地区的应用. 华北地震科学. 2021(02): 40-47 . 
本站查看
2. 蒋一然，宁杰远，李春来. 川滇地区地震分布及地壳结构的双差地震层析成像. 华北地震科学. 2021(02): 17-26 . 本站查看
3. 石永祥，蒋一然，宁杰远，李春来. 基于震源聚类方法确定川滇交界东部地区微震的空间分布特征. 华北地震科学. 2021(02): 10-16 . 本站查看
其他类型引用(1)
计量
- 文章访问数: 2323
- HTML全文浏览量: 1380
- PDF下载量: 36
- 被引次数: 4
