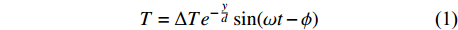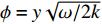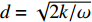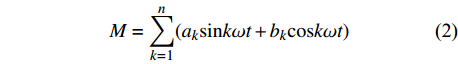0   引言

长期的形变连续观测要求具有良好的洞室条件。只有温度、湿度、气压、大风等因素影响小，地表噪声小，才能产出高精度的形变资料。在诸多的影响因素当中，温度条件的影响无疑是重要因素之一。国内外已在此方面开展了不少的研究分析工作，众多研究者从理论模型和实际观测方面进行了深入分析。曹建玲等^[1]利用有限单元法定量研究了地形起伏条件下的地表温度年变化对形变倾斜及应力的影响；孙玉军^[2]等利用有限元方法计算了洞室内温度年变化引起的地倾斜和地应变，即洞温变化0.2 ℃时，可以引起20 ms量级的地倾斜和10⁻⁷量级的地应变。从实际观测方面，如陆德明^[3]对常熟台、赵爱平^[4]对九江台、樊冬^[5]对淮北台、徐甫坤^[6]对昆明台、高昂^[7]对北京香山台等进行观测研究，都得出“台站要进一步采取措施，减少洞温的年变化，才能提高观测质量”的结论。

怀来地震台历年来十分重视洞室的密封、保温工作。形变山洞具有独特的保温覆盖层，岩性是太古界桑干群混合岩和花岗片麻岩，洞室上方有28～32 m第四系黄土。由于黄（干）土的热扩散率是花岗岩的1/4，相当于厚1 m黄土可起3 m多花岗岩覆盖体的作用，即相当于80 m以上的花岗片麻岩体覆盖^[8]。洞室进深180 m，各仪器有相对独立的洞室，再采用聚苯乙烯泡沫板和塑料薄膜“全封闭”式覆盖。2018年的台站标准化改造对原洞室水泥门进行更换，又增上五道密封门，加强山洞密封。该台站应用国家台网管理中心配置精度为0.05 ℃的TCM-3型测温仪进行洞温观测，2019年洞温有效年变幅为0.06 ℃，日变幅为0.01 ℃，低于年变幅度0.5 ℃、日变化幅度0.03 ℃规范要求，其热稳定性居全国前列。在这样密封保温的洞室中，洞温曲线看似一条直线，故每次落实形变异常总认为洞温恒定，温度对倾斜、应变观测无干扰，以致无法做进一步分析研究工作。实际上，形变观测仪器所处的洞室温度是否有微弱变化及其变化规律如何，其与洞外气温、气压是否相关以及洞温变化对形变观测有何影响等等，这些问题均需高精度的洞温仪进行实测，这远比理论模型计算可靠，对识别形变资料异常更有实际意义。

1   仪器研发

2019年7月初怀来高精度洞温仪设计制作完成，其主要有以下特点：①采用标准的modbus通信协议，可以进行多点测量，便于进行数据比测验证；②采集软件自主编写，便于调试和接入不同的传感器，可同时测量温度、气压、湿度等；③温度探头高分辨率，达到 0.000 1 ℃，能看出日变幅为0.01 ℃洞温曲线变化过程；④数据输出遵循“十五”地震通讯协议，分钟采样，提供FTP、网页和命令3种通讯模式，进行数据存储、下载、时钟校对、仪器管理控制等。

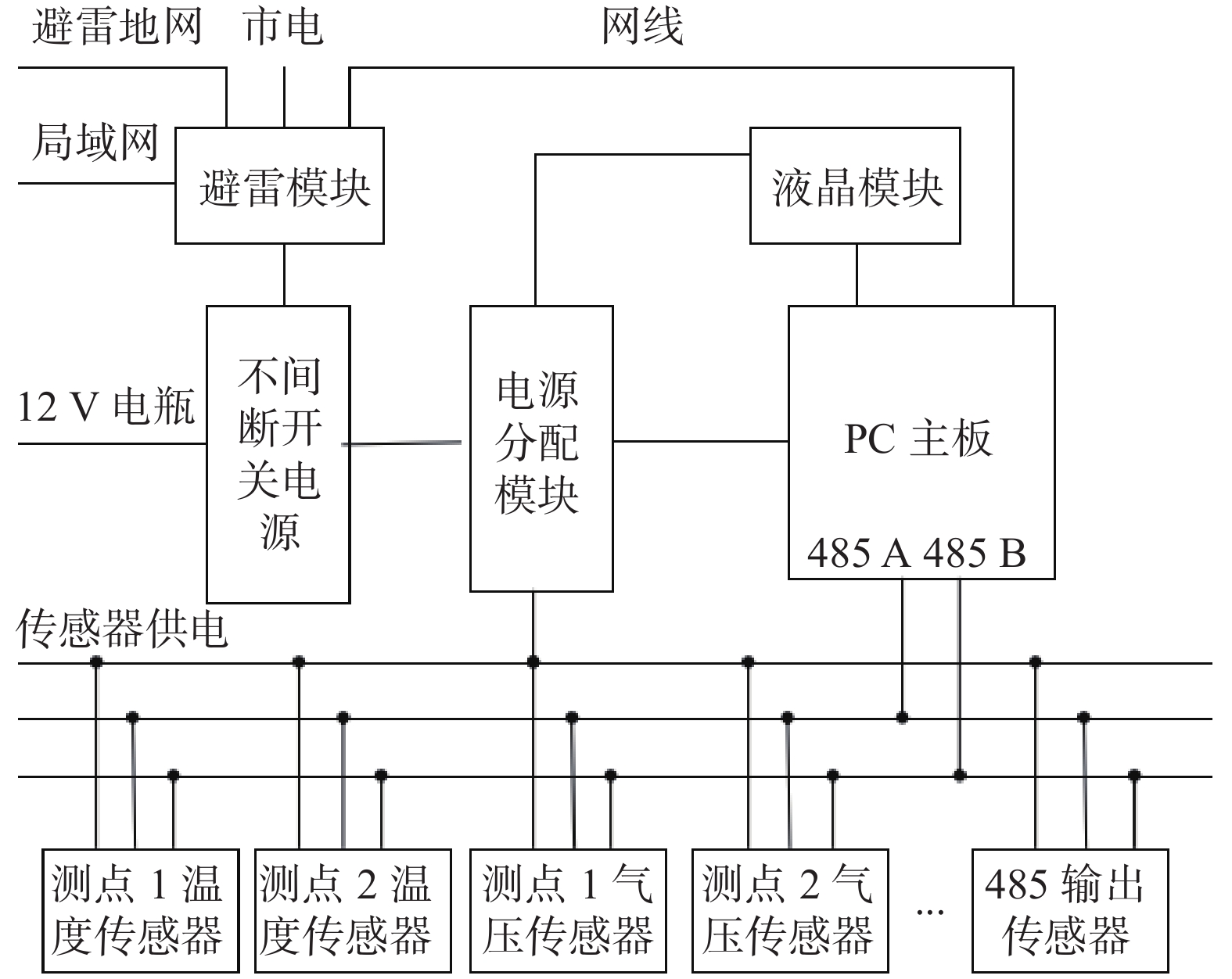
仪器采用模块化设计，主要由PC主板、电压分配模块、不间断开关电源、避雷模块、显示屏等构成。主板选用低功耗PC104主机，安装XP系统，下位机，通过串口和温度、气压传感器进行485通讯（图1）。

图  1  多点高精度气温、气压观测仪结构图

下载: 全尺寸图片 幻灯片

温度传感器采用微型机械加工、精良电路设计，以C8051F350单片机作为控制核心，铂电阻PT1000作为温度探头，具有抗振动、稳定性好、准确度高、耐高压而且线性度好的特点。

1）四线制，在热电阻的两端各连接2根导线的方式，其中2根引线为热电阻提供恒定的电流I，把电阻R的变化转换成电压信号U的变化，再通过另2根引线将U引至输出，可完全消除引线的电阻影响。

2）有效解决自热效应。根据元件发热公式P=I²R，为减少电流流经铂电阻产生的热量对测量温度的影响，采用1 mA恒定电流、间歇供电的方式，整个电路板采用防水绝缘密封胶灌装而成，解决了自热效应，适合潮湿山洞观测。

3）抑制元器件参数“零点”对“放大倍数”的影响。

4）加入2个参考电阻，有效消除了恒流源以及基准源电压不稳产生的误差。参考电阻R₁和R₂采用定制的精度为0.5‰、温度稳定性5 ppm的精密电阻。

气压传感器选用气象站专供大气压力变送器，由电源模块、变送模块、数据处理模块构成，抗干扰能力强，性能可靠，响应速度<1 s，测量精度优于±1%。

2   仪器布设

仪器初步设计完成后，对气压传感器和温度传感器进行了比测校准。标准气压计采用气象局校准精度为0.1 hPa的气压计；标准温度计采用精度为0.05 ℃的水银温度计，校准误差要求<0.5%。2019年8月在山洞NE向入口、伸缩仪EW向传感器近处分别放置了温度传感器和气压传感器，在水管仪N端、S端近处放置了气压传感器，产出观测数据。

经实验数据对比，洞内外气压测值时间变化基本同步，幅度基本一致。经多次查漏补缺，不放过每一个小气孔，试图把洞室做最严格密封，但洞内外气压数据仍完全一致，即目前台站所做的密封工作，不能阻止洞内外空气对流，层层密封包裹的形变仪器所受气压干扰洞内外基本一致。

3   洞温实测特征

3.1   洞温日变化

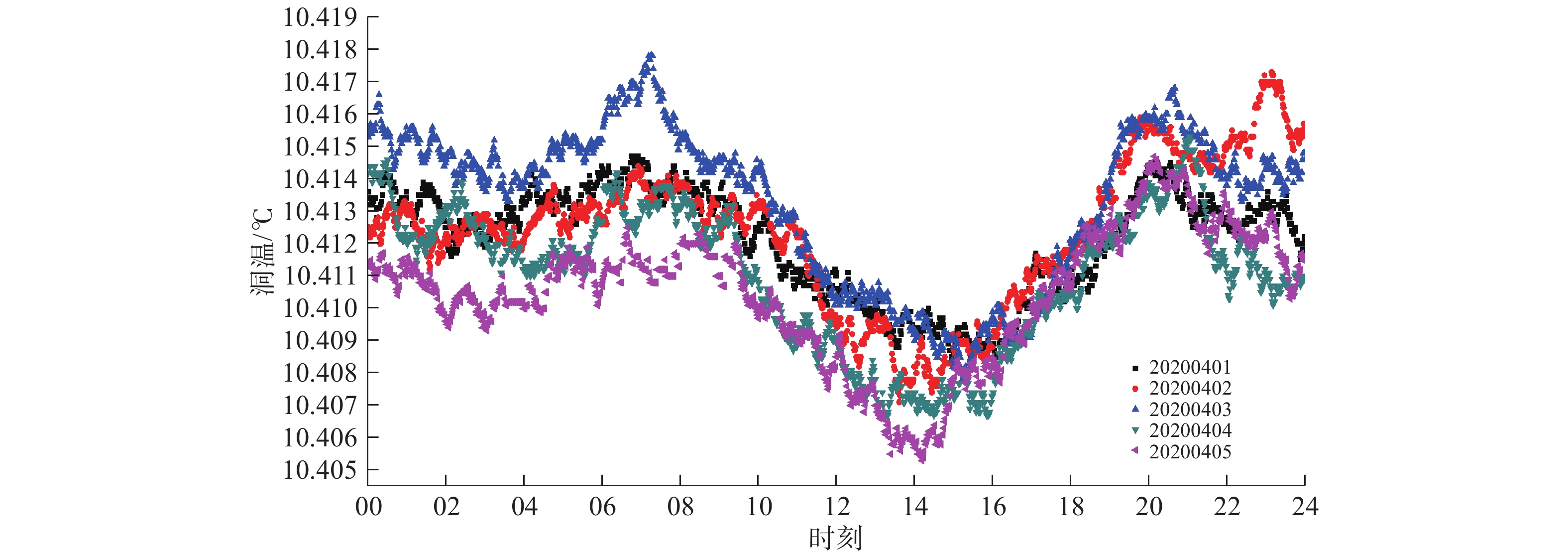
图2为2020年4月1—5日怀来台洞温分钟值图。观测表明，高分辨率下的洞温数据随时间而改变，是准周期性的正弦波动。一天当中，总有一个最低值，一般出现在14—15时，2个高值分别出现在上午7—8时和晚上20时左右，凌晨3时为次低值，日变幅平均为0.008 ℃。

图  2  怀来台洞温日变曲线图

下载: 全尺寸图片 幻灯片

当地表水平、介质均匀的情况下，深度y处所引起的地下温度变化的解析解^[9]为：

式中： ΔT为地表温度变化幅度；$\phi = y\sqrt {\omega/2k} $ 为地表温度与深度y处温度波动的相位差；趋肤深度$d = \sqrt {2k/\omega } $，即温度变化振幅随深度增加指数减小，在深度d衰减到表面值的1/e，且相位比地表滞后1 rad。如果取年周期性变化角频率ω=2×10⁻⁷ rad/s，热扩散系数k=1×10⁻⁶ m²/s，地表温度变化为40 ℃时，引起地下20 m深度的温度变化幅度为0.071 7 ℃，若取日变化角频率ω=7.3×10⁻⁵ rad/s，计算日变幅度为1.71×10⁻⁵¹ ℃，则可以完全忽略不计。实测洞温日变呈正弦波动变化，只是幅度比理论计算值大很多。

3.2   洞温月曲线变化

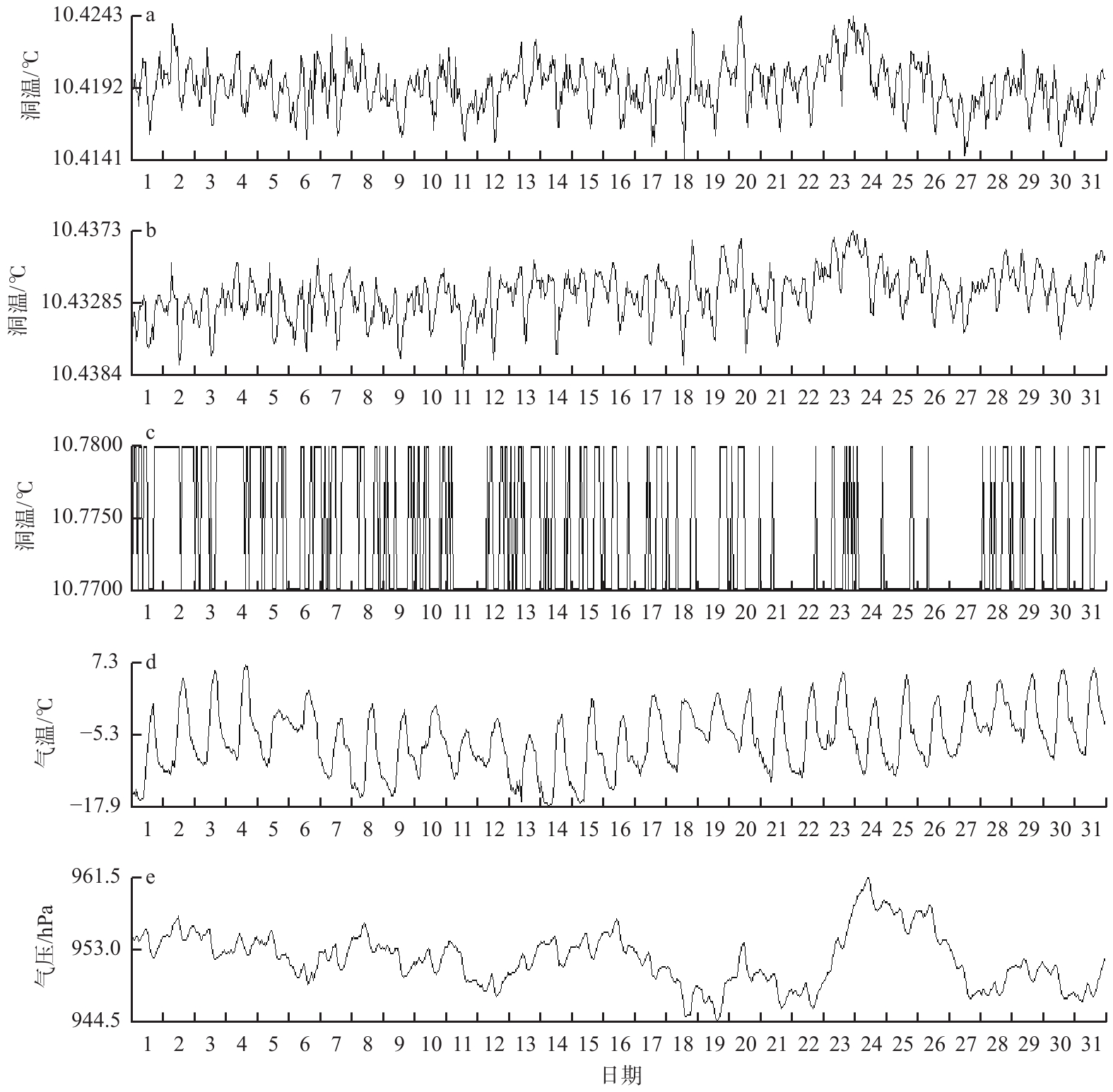
2020年1月洞室无人为进出干扰，绘制月整时值见图3。其中，图3a为传感器置于NE向斜边洞室外端洞温整时值图，月变幅为0.011 0 ℃，日变幅最大为0.010 8 ℃，最小为0.005 3 ℃；图3b为传感器置于EW向伸缩仪小腔体内整时值图，相较于图3a处多了两层泡沫板和塑料膜，是山洞保温环境最佳处，月变幅为0.008 9 ℃，日变幅最大为0.009 6 ℃，最小为0.004 8 ℃；图3c为台站上报国家台网中心TCM-3型洞温仪记录数据，传感器在EW向洞室，月变幅为0.01 ℃，数据在10.77、10.78间切换，呈一条宽幅直线；图3d为台站RTP-Ⅱ型气象仪记录的室外气温曲线，月变幅为25.2 ℃，日变幅最大为19.0 ℃，最小为7.6 ℃；图3e为台站RTP-Ⅱ型气象仪记录的室外气压曲线，月变幅为17.0 hPa，日变幅最大为5.8 hPa，最小为3.0 hPa。

图  3  怀来台2020年1月布设NE、EW向洞室的洞温、TCM-3洞温、气温、气压整时值图

下载: 全尺寸图片 幻灯片

对2020年1月洞温、气温、气压整时值作相关分析：

以日分段计算2处测点洞温相关系数，数值为0.805～0.962之间，整体pearson相关系数为0.894，相关性显著。图3a和3b曲线形态极其相似，可同步反映山洞温度变化。

以日分段计算洞温和气温相关系数，数值为0.054～−0.824之间，整体pearson相关系数为−0.485。由洞温日变化特征，每天14时左右洞温最低（图2），而这个时段气温通常是每天最高值，二者正好相反，这是负相关的数学释义。按照常规推测，二者应该变化一致，或者室外气温经空气对流、洞体传导热传递，时间可能滞后几小时。负相关系数表明怀来山洞保温条件较好，洞温基本不受外界气温影响。由图3a、3b和3d可见，气温曲线形态上是单峰走势，而洞温曲线呈双峰状态，气温每日形态变化较大，日变幅较大，洞温则相对稳定，变化近似于等幅，洞外较大的气温变化形态并不能经几小时后传递给洞温，洞温曲线是一种“独立”的准周期状，明显区别于气温。

以日分段计算洞温和气压相关系数，数值为0.263～0.783之间，整体pearson相关系数为0.495，即气压为正相关。在置信度（双测）为0.01时，相关性是显著的。

洞温和气温、气压作回归分析：

洞温=10.2517−0.00015×气温+0.00018×气压

其中：气温标准化系数为−0.430，气压标准化系数为0.302，复相关系数为0.546；调整后拟定系数为0.297，标准误差为0.001 764，二者均通过0.05显著性检验。

3.3   洞温的周期分析

原理：假设复杂动态的周期函数为M=f（t），那么可由正弦和余弦项组成的傅里叶级数作为周期函数的表达式，即

式中：cosωt或sinωt为基波，为k次谐波或为1/k分波，其周期为基波周期的1/k倍（k=1，2，…n）。求解该方程的关键是求得a_k和b_k两个系数，该系数可用最小二乘法求解^[10]。

对2020年1月洞温进行周期分析（表1）。怀来洞温序列主要有16个周期成分，其中11个周期用t检验为显著相关。把这些周期数据进行叠加，和原始数据作相关分析，复相关系数为0.939 1，残差标准差为0.119 0，回归方程F检验值为177.522 8，显著性水平0.01的F临界值为2.024 85。显著性水平0.05的t临界值为1.963 22，显著性水平0.01的t临界值为2.582 61。

表  1  怀来台洞温周期分析成分表

序号	主要周期/小时	偏复相关系数	t检验值	结论
1	12.0	0.213 92	5.906 48	特别显著
2	24.0	0.163 40	4.465 82	特别显著
3	8.0	0.154 01	4.202 68	特别显著
4	74.4	0.134 55	3.661 24	特别显著
5	248.0	0.126 52	3.438 99	特别显著
6	124.0	0.119 48	3.244 78	特别显著
7	106.3	0.108 74	2.949 44	特别显著
8	62.0	0.105 31	2.855 37	特别显著
9	6.0	0.103 98	2.818 89	特别显著
10	46.5	0.103 33	2.801 14	特别显著
11	53.1	0.096 64	2.617 92	特别显著
12	186.0	0.095 28	2.580 83	显著
13	372.0	0.093 38	2.528 96	显著
14	93.0	0.092 26	2.498 19	显著
15	4.0	0.088 81	2.404 01	显著
16	67.6	0.087 15	2.358 92	显著

下载: 导出CSV 

| 显示表格

洞温变化可分为周期性变化和微变化两种，正常情况下主要为周期数据。高精度洞温观测接近于流体学科的地热温度观测。在一些条件较好井孔，随着观测精度的提高，记录到井水温度的潮汐效应，井水温度的日起伏与重力理论固体潮的起伏一致^[10]。图4a～4d分别为2020年1月重力固体潮理论整时值、洞温整时值、主要周期成分叠加和残差值。怀来洞温作为辅助观测，山洞环境远不如地下井水温恒定，受到很多因素干扰。从曲线来看，周期性变化和重力理论固体潮的起伏一致，具有同步变化特征。

图  4  怀来台2020年1月重力固体潮理论值和洞温周期分析图

下载: 全尺寸图片 幻灯片

3.4   洞温的振幅谱分析

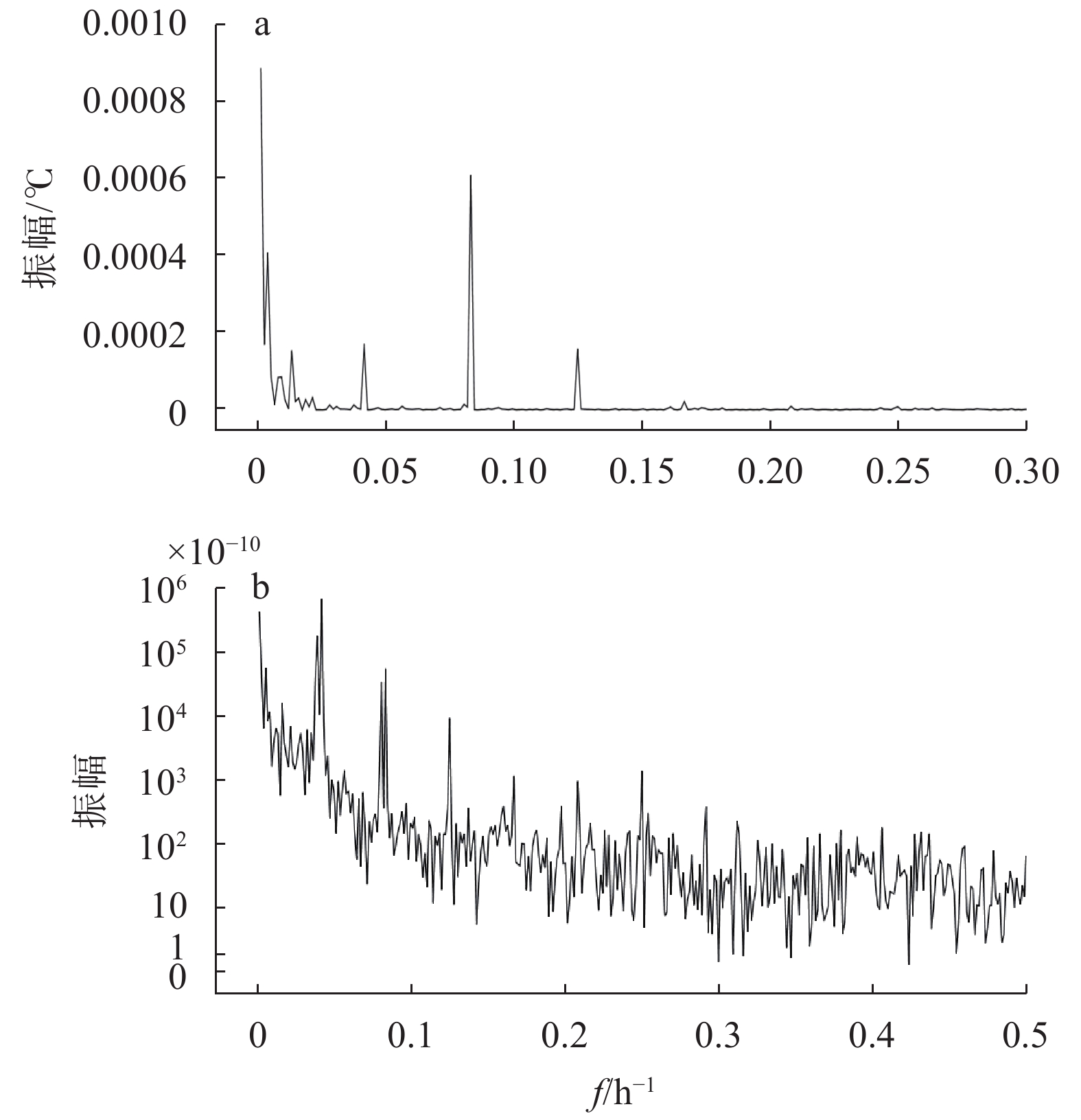
应用SPSS软件对2020年1月洞温整时值数据进行频谱分析，结果如图5a。其中：日波S₁的初始频率f₀=0.041 666 7 h⁻¹，振幅Am=1.712 46×10⁻⁴；半日波S₂的初始频率f₀=0.083 333 3 h⁻¹，振幅Am=6.104 11×10⁻⁴；1/3日波S₃的初始频率f₀=0.125 h⁻¹，振幅Am=1.590 63×10⁻⁴；1/4日波S₄的初始频率f₀=0.166 7 h⁻¹，振幅Am=2.222 22×10⁻⁵。可见，洞温半日潮振幅最大，日潮次之，1/3潮振幅最小，这与固体潮理论是一致的^[11]。图5b为怀来2020年1月伸缩仪EW向频谱分析图。倾斜、应变固体潮观测中M₂波为卓越周期12.38 h，波振幅最大，而洞温频谱中频率f₀=0.080 504 7 h⁻¹，即周期为12.42 h最接近M₂波的周期，振幅Am仅为1.438 23×10⁻⁵，不是很明显。

图  5  怀来台洞温、伸缩仪EW向频谱分析

下载: 全尺寸图片 幻灯片

仪器记录到的洞温潮，准确些应叫作地温潮，反映山洞中岩体所受的温度变化，区别于固体潮、海潮和大气潮。

3.5   洞温的主要干扰因素

洞体温度主要包含山洞内空气温度变化和岩体温度变化。岩体温度的影响因素主要有太阳的热辐射、地壳岩石的放射生热、地球的重力热及月球影响的潮汐热, 在几百公里内可以认为这种变化是均匀的^[12]，这也是前面分析的主要周期成分。而洞温微变化，即随机或短期干扰的主要有人为进洞、洞室中观测仪器散热、气压骤变等。

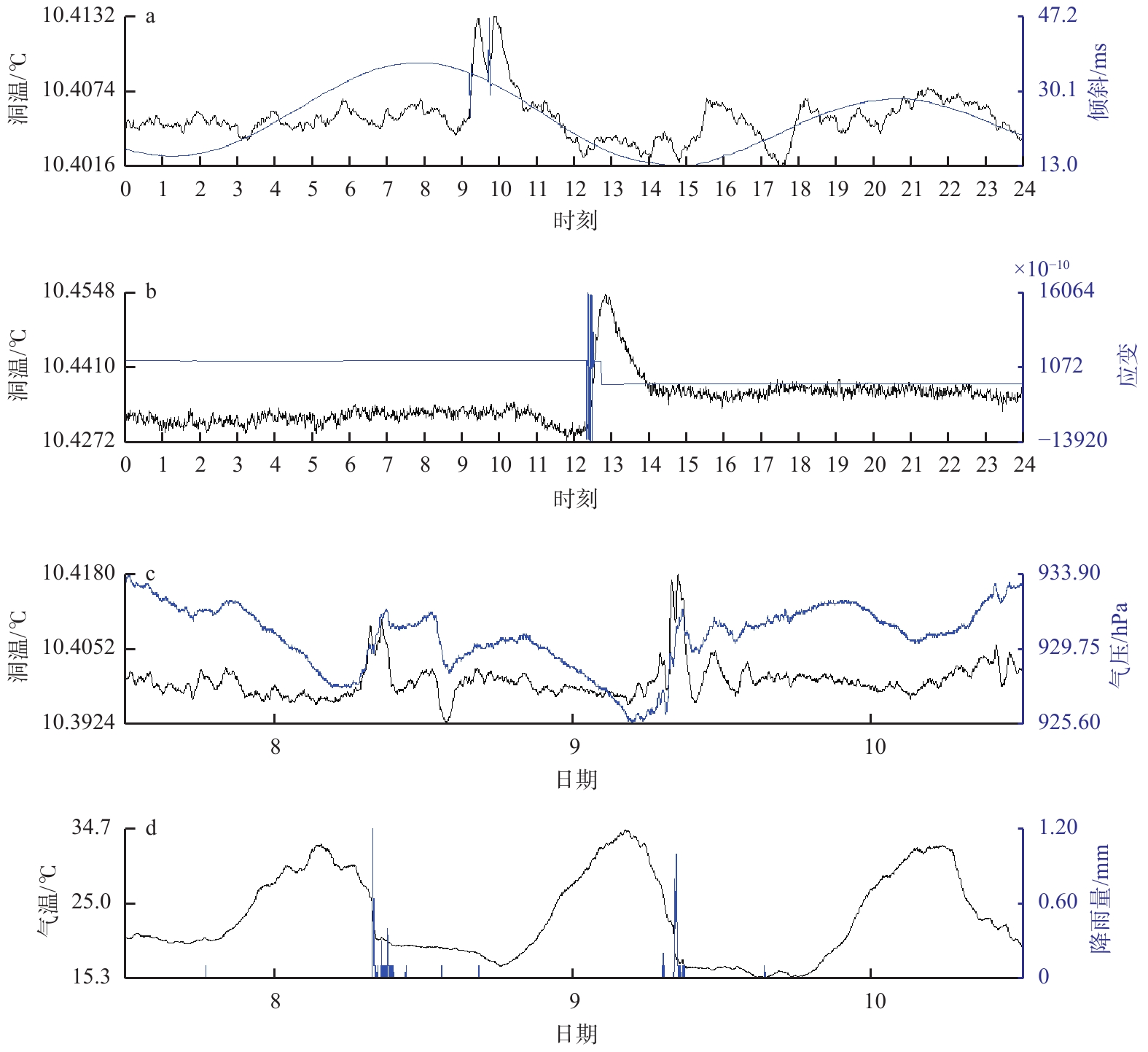
1）人为进洞。2020年7月5日一名观测人员进洞检修仪器，9时14分经NE向洞室进入NS向洞室，9时44分出洞，温度探头距离过道约1 m，悬空放置。从图6a洞温曲线可明显看出人员进出的整个过程，路过探头附近时引起温度上升约0.007 ℃，之后逐渐恢复。水管仪NE向同时记录到干扰，主要由地面振动引起，不是温度干扰。

图  6  怀来台洞温受干扰变化图

下载: 全尺寸图片 幻灯片

2）标定电机转动。2020年3月31日伸缩仪EW向12时20分至13时31分进行标定，温度探头距离标定电机约0.2 m，电机转动引起周围温度同步变化，上升约0.025 ℃（图6b）。这是易忽略的工作细节，一般不会引起重视，原TCM-3洞温仪记录曲线无变化，同时也表明新布设的洞温仪能够反映极微弱的温差变化，数据是可信的。

3）气压骤变。大风、寒流、降雨、高温等极端气象变化必然引起气压骤变，故此处归纳为一类。2020年 8月8日19—23时、9日1—5时、19—21时、10日3—4时内有降雨（图6c），降雨前后气压有突变，洞温受干扰明显，呈同步变化。

空气对流交换，必然引起气压和温度变化；温度和气压一定条件下相互影响、关系复杂，很难做定量分析。在开放的环境下，温度越高气压越低，在密闭的环境下（体积不变），温度越高气压也越高。山洞环境相对密闭，故洞温和气压成正比。如前所述，洞内外气压同步变化，洞温也会同步变化，进而影响形变仪器。

4   洞温对形变观测的影响

4.1   洞温对应变日值变化的影响

温度变化会引起洞体里岩石体积发生膨胀与收缩，从而引起应变观测的拉伸与收缩，造成对伸缩仪曲线短期畸变或干扰。

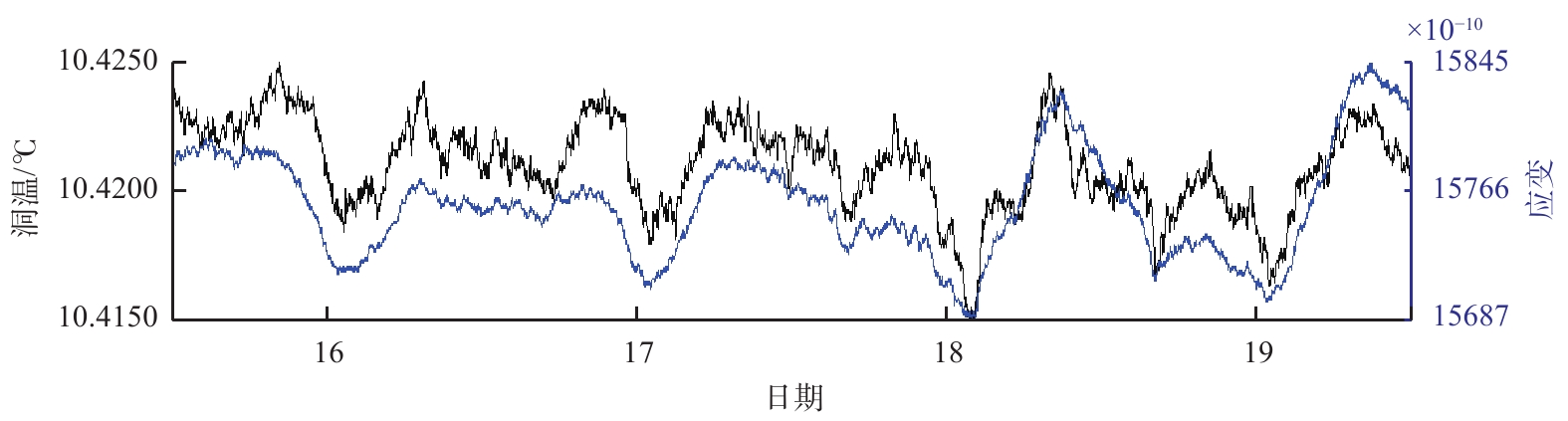
怀来台洞体应变EW向一直以来精度较低，固体潮形态较差。怀来台洞温和伸缩仪EW向2020年1月16日—19日分钟值图（图7）中，这些曲线毛刺或固体潮畸变，通常认为洞室条件不是很优越，或是仪器工作不稳定、线路接触不良、气压干扰等几种原因造成，和洞内温度关系不大。因为原洞温观测数据几乎恒定，呈直线状，对比布设的洞温曲线，可以看到洞温波动与伸缩仪EW向观测曲线很好的对应关系，应变和洞温几乎同步变化。这几日属小潮日，即农历廿二至廿五，固体潮理论值相对较小，洞温影响效果较突出。经查看本台伸缩仪EW向日变曲线有干扰、畸变的时段，多数能在洞温曲线上找到对应变化。

图  7  怀来台2020年1月16—19日洞温和伸缩仪EW向分钟值图

下载: 全尺寸图片 幻灯片

图7中洞温波动幅度为0.010 1 ℃，相应的应变量高频波动幅度达158×10⁻¹⁰，计算二者的相关系数为0.89，存在明显的正相关。洞温的微变化引起洞室岩体和仪器主体铟瓦棒长度的微变化，用“热胀冷缩”原理解释最为直接简单，即洞温升高，洞内岩体和铟瓦棒拉伸，观测数值变大；反之，洞温降低，呈压缩状态，数值变小。温度变化是伸缩仪EW向短时间固体潮畸变的直接原因。

4.2   洞温对应变观测的趋势性影响

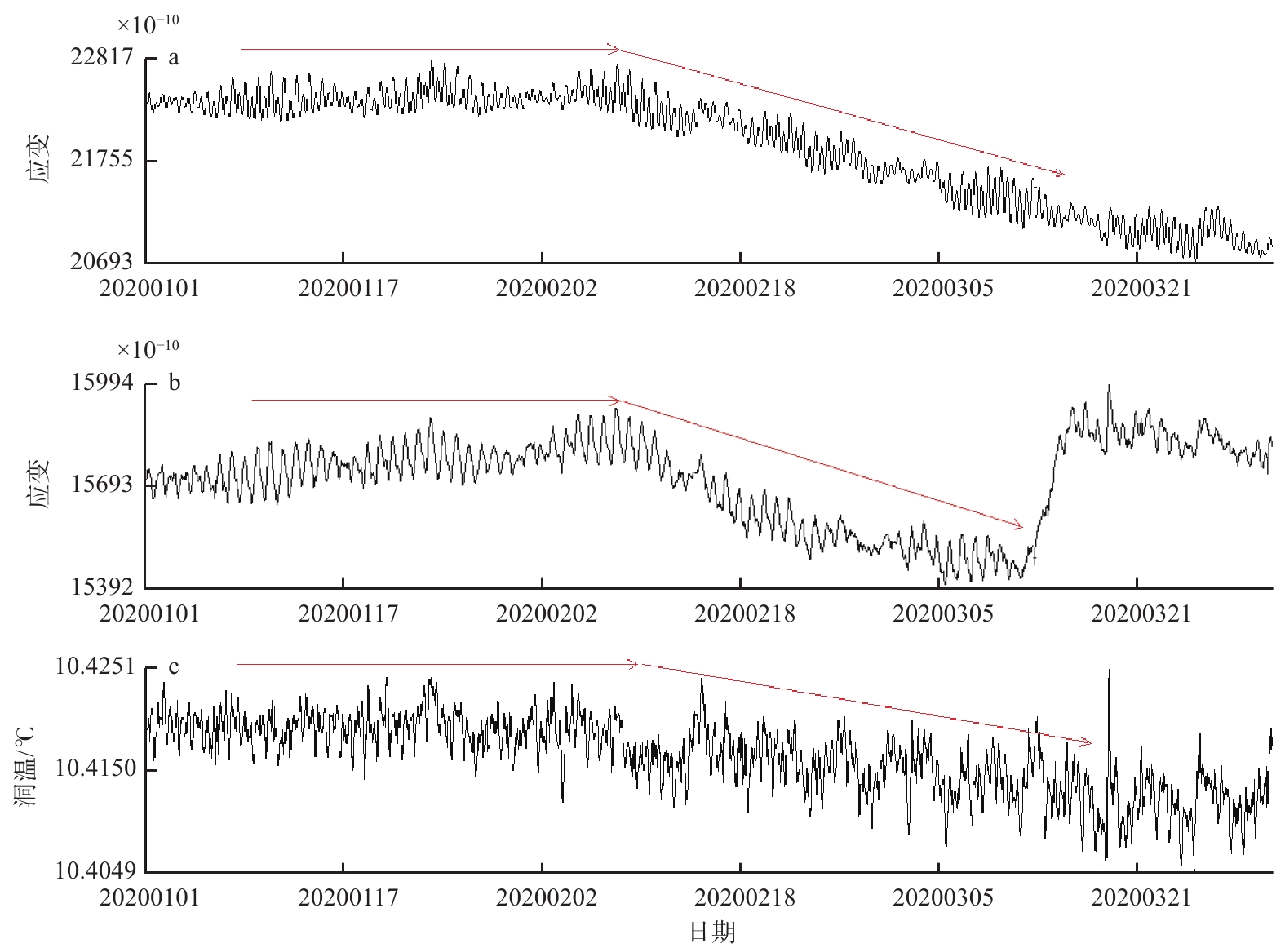
怀来台洞体应变伸缩仪NS、EW向观测曲线在2020年2月10日发生趋势性转折（图8），伸缩仪由平稳状态都转为压缩加速。根据应变受力模型，一个地区有主应变主轴方位受压，与其垂直的剪应变则为拉伸方向，这点从台站多年的观测曲线得到验证。此时NS、EW向应变观测都表现为受压状态，呈集中受压形态。查看台站前几年曲线都有相同变化，只是时间先后略有差异，故一直认为是年变，缺乏合理的解释。对比观测的洞温曲线，洞温不是随着春季到来温度升高，而是从2月10日起呈降低趋势，到3月31日下降约0.010 5 ℃，同样用“热胀冷缩”原理很容易解释伸缩仪和体应变的趋势转折了，也找到了多年来“这些转折是年变”的根本原因。

图  8  怀来台2020年1月1日—3月31日伸缩仪NS、EW向和洞温分钟值图

下载: 全尺寸图片 幻灯片

5   结论与讨论

1）为完成高精度的洞温及气压观测，仪器硬件采用成熟的模块设计组装，按照数字地震观测网络技术规程设计，并独立开发了软件应用程序，具有低成本、低功耗、安装方便的特点，达到了实验设计目的，也适合其他台站或测点应用。

2）仪器在怀来台密封保温的山洞中布设，观测到洞温日变化曲线具有周期性的潮汐效应，可反映洞室岩体的温度特征。封闭洞室中温度和气压变化相关，洞温对伸缩仪日变曲线干扰明显，并引起台站应变观测趋势性转折。精确掌握形变仪器所处的温度环境要比和洞外气温做相关分析更准确，对认识形变观测规律和异常识别更有帮助。

3）为了减少干扰，提高形变观测内精度，各台站对形变洞室的保温密封措施不断加强，洞温变化越来越小。只有投入高精度的洞温仪观测，才能记录到有效的温差变化，才能更好识别形变观测中的畸变干扰或异常。建议今后利用好现有洞室条件，使洞温观测能反映地下岩体温度，反映应力应变情况，即“热测应力”^[13-14]。

4）由于台站条件所限，没有精度达到0.000 1 ℃的校准仪器，测试环境也很难模拟温度的微变化。和倾斜、应变观测一样，洞温测量仍属于“绝对测量方法，相对测量系统”^[15]。建议本仪器及台站的洞温观测都实现精确校准，达到规范化、标准化要求。