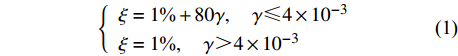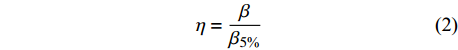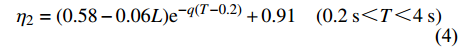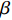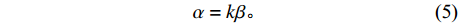Influencing Factors of Variable Damping Ratio Response Spectrum of Shallow Buried Subway Station Structure
-
摘要:
以单层双跨结构为研究对象，建立变阻尼比条件下的平均化反应谱，并对其进行回归分析，对该平均反应谱即水平地震影响系数曲线进行了特性分析。结果显示，该平均化反应谱与地铁车站结构所在的围岩性质、地震波频率特性、场地设防烈度以及车站埋深有关：在不同设防烈度条件下的变阻尼比相对反应谱形状是不同的，而且设防烈度越高，反应谱峰值越低，图形形状越矮；在围岩参数发生改变时，泊松比对反应谱的变化影响最大，峰值影响与反应谱曲线形状差异性最大；随着埋深的增加，各类场地土的影响系数峰值逐渐减小；地震波频谱特性引起的结构动力反应得到的地震影响系数随地震波傅里叶谱的峰值增大而增大。
Abstract:Taking single-layer double-span structure as the research object, the average response spectrum under variable damping ratio is established, and its regression analysis is carried out. The characteristics of the average response spectrum, that is, the horizontal seismic influence coefficient curve, are analyzed. The analysis shows that the average response spectrum is related to the surrounding rock properties, the frequency characteristics of seismic waves, the intensity of site forcement and the depth of the station. The shape of the relative response spectrum of variable damping ratio is different under different fortification intensities. The higher the fortification intensities, the lower the peak value of the response spectrum and the shorter the shape of the graph. When the surrounding rock parameters are changed, Poisson's ratio has the greatest influence on the change of the response spectrum, and the difference between the peak value and the shape of the response spectrum curve is the greatest. With the increase of burial depth, the peak value of influence coefficient of all kinds of site soil gradually decreases. The seismic influence coefficient obtained from the structural dynamic response caused by the spectral characteristics of seismic waves increases with the peak value of the Fourier spectrum of seismic waves.
-
Keywords:
- surrounding rock /
- earthquake /
- response spectrum /
- intensity of fortification /
- subway station
-
0 引言
地震发生时，对建筑物或构筑物结构动力反应产生重要影响的因素为地震动的震幅、频谱和持时。振幅一般指地震加速度、速度或位移的峰值，由于加速度a的大小可以表示地震动的强弱，而且与质点运动的惯性力相联系，因此中国抗震规范均采用水平地震加速度作为衡量地震动振幅的指标。反应谱是在给定地震动作用期间，单质点体系的最大位移反应、最大加速度或最大加速度反应随质点自振周期变化的曲线。即同一阻尼比下，不同周期的场地在某地震波作用下的最大加速度反应、加速度反应谱与场地的类别息息相关。
其中，建筑物的阻尼性能对其振动反应有重要影响，阻尼比是反映结构阻尼性能的主要参数。GB50011—2010《建筑抗震设计规范》（2019修订版）(以下简称现行规范)的地震作用计算中，考虑了阻尼比变化对反应谱曲线的影响。
随着中国经济的快速发展，越来越多的人开始研究阻尼对设计谱的影响。王亚勇等[1]研究了不同阻尼比情况下长周期段反应谱的特性，提出不同阻尼反应谱可以通过对阻尼比为5%的谱调整得到；张椿民[2]基于一维场地分析采用整体式反应位移法和等效线性化时程分析法对地下二、三、四层地铁车站进行了结构抗震分析，结果表明：通过一维场地分析方法确定的土层参数以及基岩波能够满足整体式反应位移法和等效线性化时程分析法的输入条件；李春锋等[3]对台湾集集地震的长周期地震动特性进行研究的结果表明，反应谱的形状主要受场地条件和震级控制，受距离的影响并不显著，近断层长周期地震动明显受断层活动特性影响，上盘的长周期地震动比下盘的强。
1 单向水平地震波反应谱分析模型
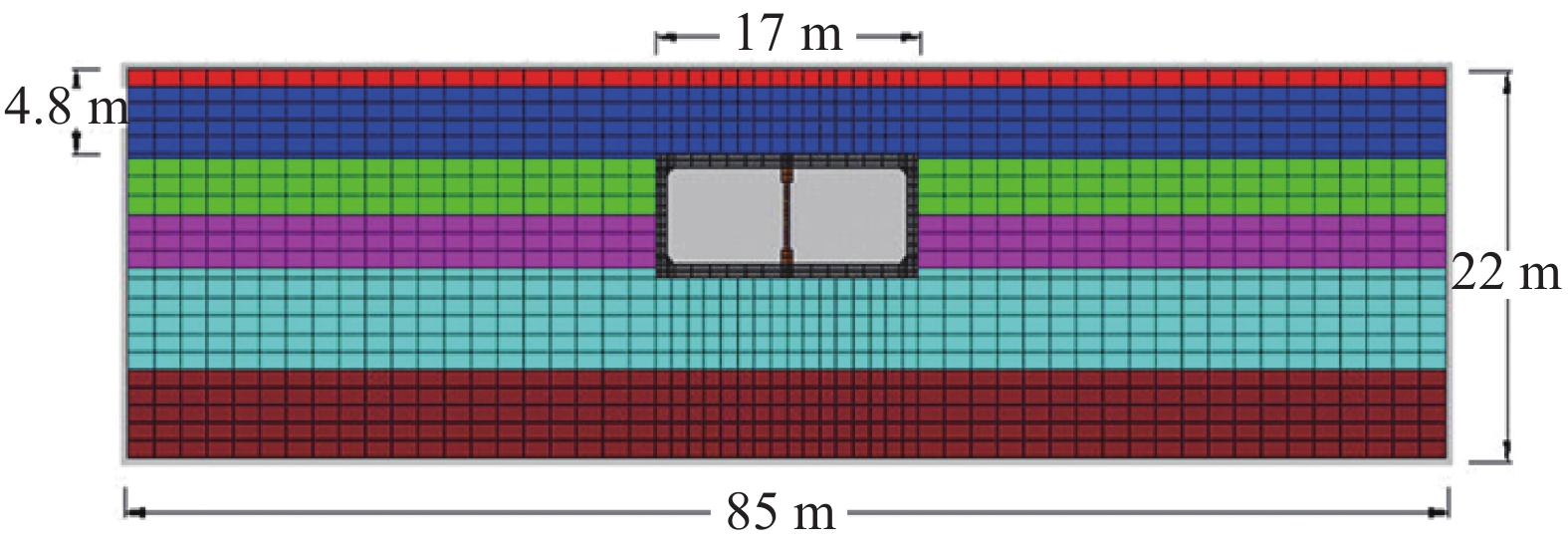
为详细研究不同阻尼比条件对结构的地震动力反应的影响，选取北京地铁单层双跨车站为研究对象，运用结构分析软件对车站主体结构的水平单向地震动力反应进行数值模拟分析，结构动力特性参数见表1。车站埋深4.8 m，模型计算范围水平方向取为85 m(5倍地铁车站宽度)[4-7]，竖向从地表取至22.2 m深度处更新世砂土层，车站的结构截面如图1所示。
表 1 分析结构的动力特性参数Table 1. Analysis of dynamic characteristic parameters of structures自振频率ω/(rad·s−1) 质量m/kg 刚度/(kN·m−1) 阻尼比ξ 93 2.79×106 9×105 0.05 ![]()
图 1 单层双跨车站横断面图(单位：mm)Figure 1. Cross-sectional view of single-storey double-span station (mm)计算模型网格化分如图2所示，北京地区各土层参数见表2，单元力学参数见表3所示。
表 2 北京地区场地土模型物理力学参数Table 2. Physical and mechanical parameters of site soil model in Beijing area土性 厚度/
m密度/
(g·m−3)体积模量/
MPa剪切模量/
MPa黏聚力/
kPa内摩擦/
(°)填土 1 1.9 101.11 38 5 15 砂土 4.1 1.9 92.89 38 2 25 砂土 3.2 1.9 136.96 56 2 28 粘土 3.1 1.9 326.62 70 18 20 粘土 2.8 1.9 241.95 111.67 20 22 砂土 5 2.0 388.92 222.24 2 38 表 3 接触单元力学参数Table 3. Mechanical parameters of contact elements最大单元尺寸/
m法向刚度/
(Pa·m−1)切向刚度/
(Pa·m−1)黏聚力/
Pa内摩擦/
(°)0.6 1×108 1×108 0 5 基岩地震波采用经过基线矫正的表4中列举的8条地震波。地震波信息如表4所示。
表 4 选取地震波记录信息汇总Table 4. Select seismic wave record information summary编号 地震波 峰值/gal 持时/s 震级 震源深度/km 1 Friuli 0.35 36 6.5 9 2 Hollister 0.19 36 5.5 7.5 3 Imperial Valley 0.31 39 6.4 8.4 4 Kobe 0.33 41 6.9 11 5 Kocaeli 0.34 35 7.4 7 6 EL-centro 0.348 56 6.9 16 7 Trinidad 0.136 21 7 20 8 汶川波 约1 ＞120 8 19 2 框架地铁地震波反应谱分析
2.1 变阻尼比条件下地震波反应谱分析
针对反应谱中阻尼理论研究的不足，考虑变阻尼比对反应谱的影响，建立基于阻尼影响系数研究变阻尼比条件下的反应谱。
根据文献[8-9]中提出的基于结构竖向广义相对剪切变形γ，针对不同结构形式的变阻尼比作为图-结构相互作用体系中结构阻尼比ξ。对于钢筋混凝土框架结构其公式为：
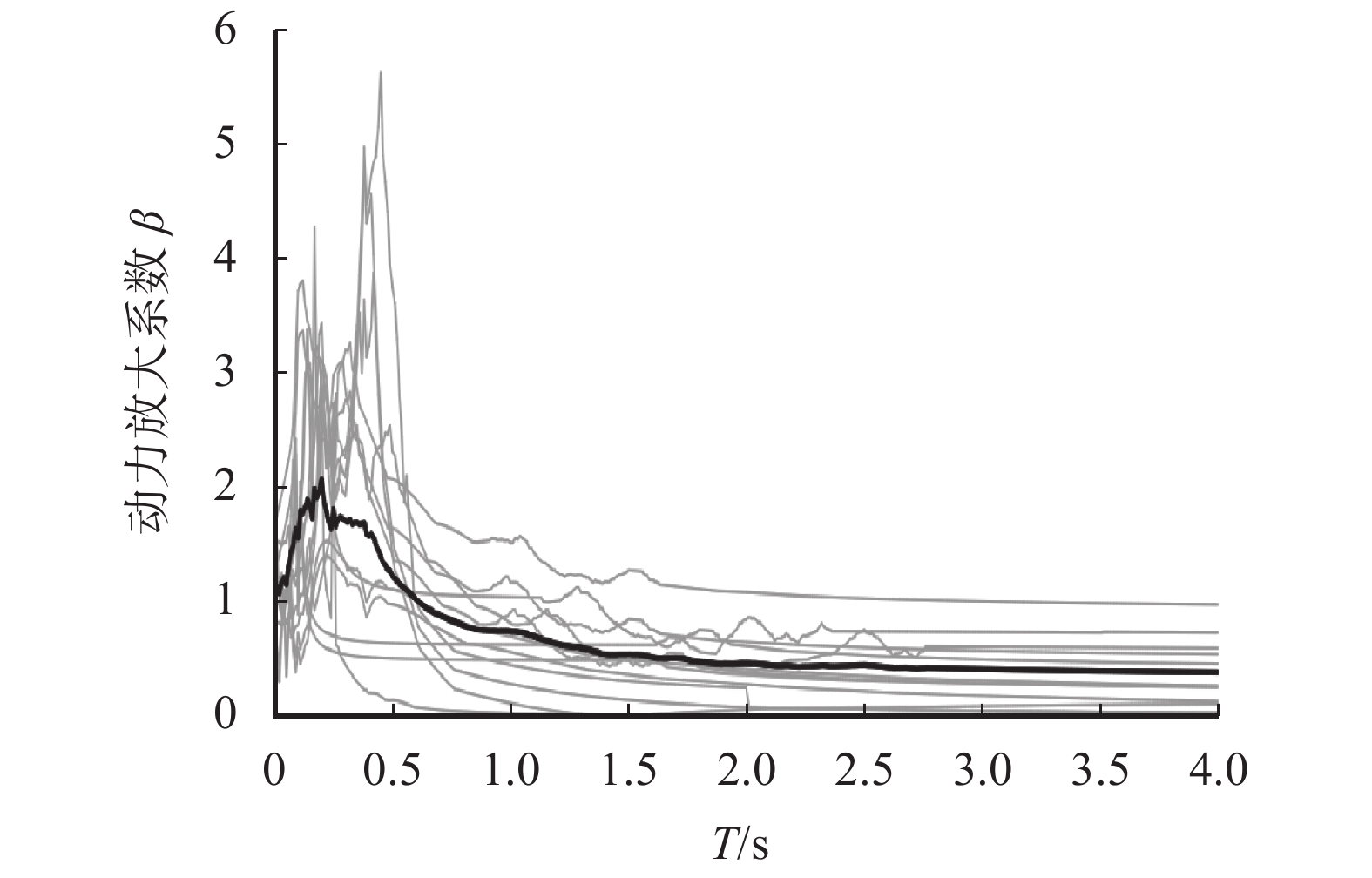
$$ \left\{\begin{array}{l} \xi=1 {\text%}+80 \gamma,\quad \gamma {\text{≤}} 4 \times 10^{-3} \\ \xi=1 {\text%}, \quad\gamma{\text{＞}}4 \times 10^{-3} \end{array}\right. $$ (1) 式中：γ为相对剪切变形。γ的取值如表5所示，从而可以得到如图3所示的在变阻尼比条件下的各地震波对应的β谱以及平均化后的β谱（图中的黑实线代表平均谱线，灰线表示各地震波对应的反应谱）。
表 5 结构相对剪切变形与阻尼比对照表Table 5. Comparison table of relative shear deformation and damping ratio of structures地震波编号 剪切应变(×10−3) 阻尼比 1 2.1 0.178 2 2.5 0.21 3 2.81 0.234 4 2.32 0.195 5 2.34 0.197 6 3.02 0.251 7 3.25 0.27 8 3.61 0.298 由图3可以看出：变阻尼反应谱的变化规律与常阻尼比条件下的谱线变化规律相近，即每条谱线也均可大致分为4个阶段：上升段、波动段、下降段以及水平段。
2.2 反应谱的阻尼修正
以阻尼比为5%时的反应谱曲线为准，其他阻尼比条件下的反应谱均以此为基础进行修正[10-11]。其中，非线性阻尼反应谱修正系数为：
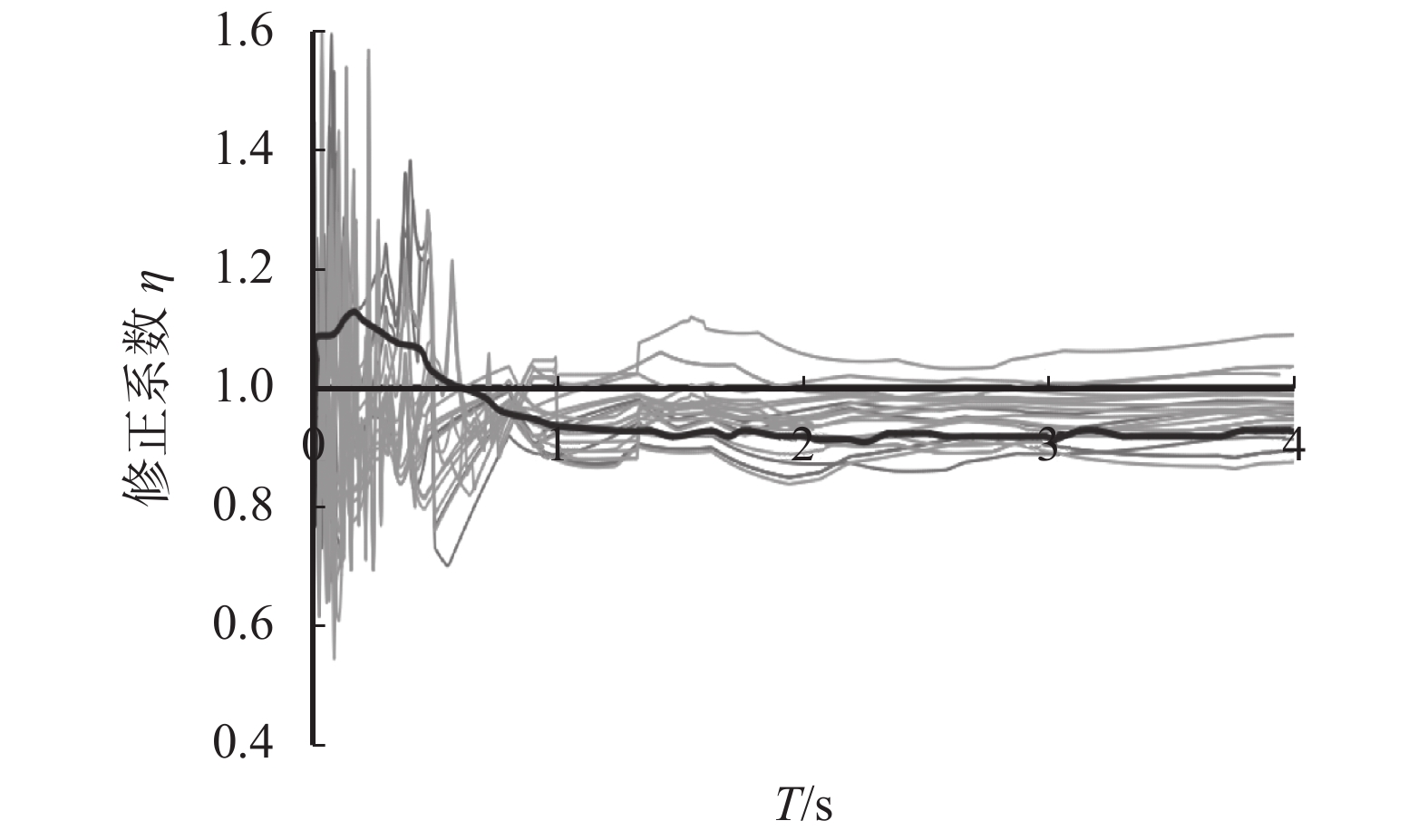
$$ \eta=\frac{\beta}{\beta_{5 {\text%}}} $$ (2) 图4为8度设防条件下，单层双跨地铁车站结构的变阻尼比修正系数曲线。图中细实线为每一条地震波作用时得到的变阻尼比修正系数曲线，粗实线为平均化的修正系数曲线。
![]()
图 4 地铁车站的变阻尼修正系数曲线Figure 4. Variable damping correction coefficient curve of subway station从图4中可以看出：当结构自振周期在0.5 s之内时，车站结构的阻尼修正系数η大于1。随着结构自振周期延长，其修正系数曲线逐渐小于1，并且趋于一个稳定值。
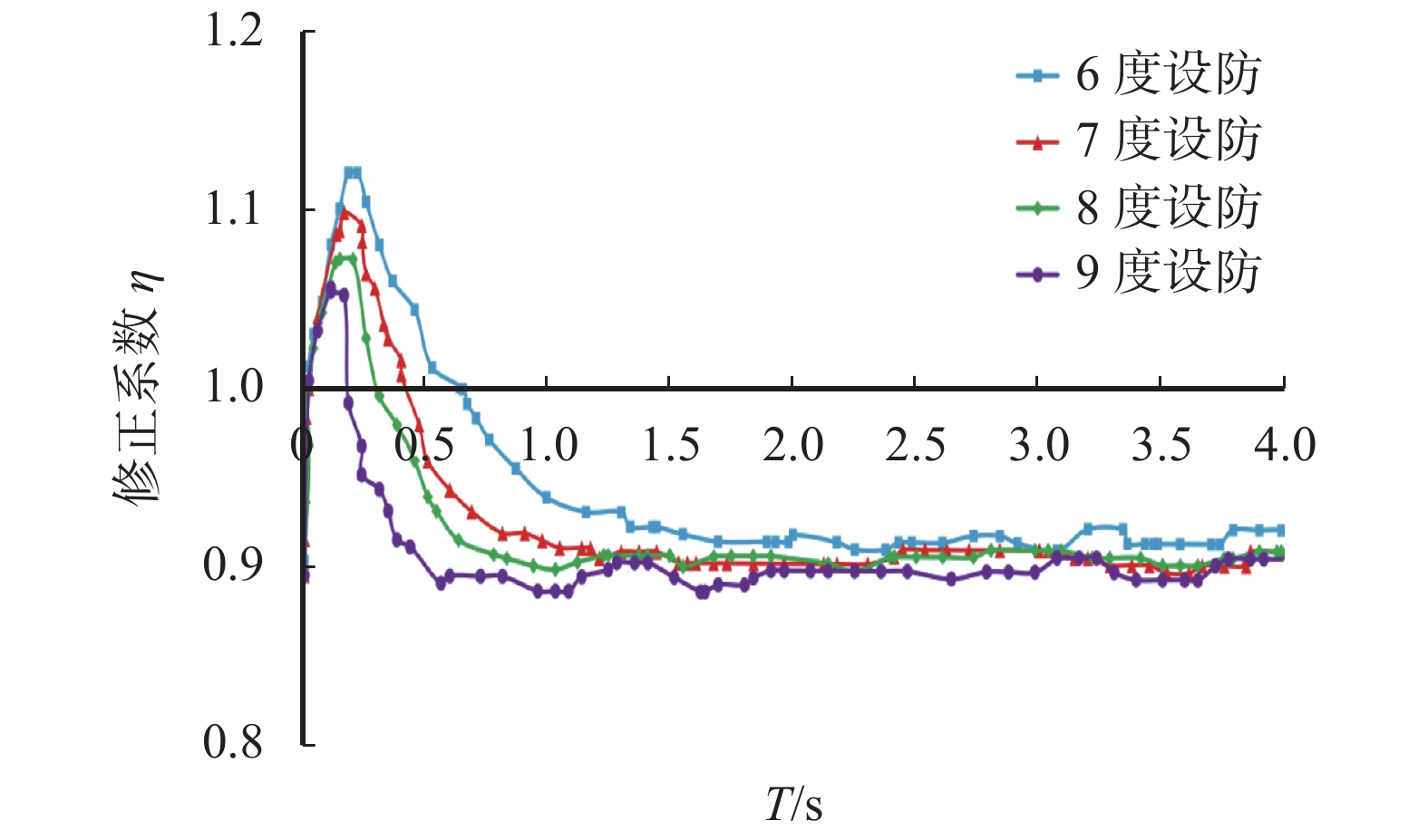
对8条地震波进行峰值修正，故按照上述与8度设防时计算阻尼修正系数同样的步骤对6、7、9度设防分别绘出η曲线（图5）。
![]()
图 5 各设防烈度下变阻尼比修正系数曲线Figure 5. Correction coefficient curves of variable damping ratio under different fortification intensities由图5可以看出阻尼修正系数曲线的特点：在0.2 s之前，呈直线上升趋势，随着设防烈度的增大，直线斜率有所减小，但仍为正值；0.2 s之后，曲线呈指数式减小，直至稳定，其稳定值为0.90～0.92，随设防烈度改变而有微小的变化。
将设防烈度和自振周期作为2个自变量建立函数，其中自振周期T为主控变量，对该修正系数进行拟合。
为便于应用，对图5中各条修正系数曲线进行回归拟合计算。根据以上修正曲线的函数特点可以得到地铁车站结构阻尼修正系数的拟合式：
$$ \eta_{1}=0.95+(1.7-0.13 L) T \quad(0{\text{＜}}T{\text{＜}}0.2\;{\rm s}) $$ (3) $$ \eta_{2}=(0.58-0.06 L) \mathrm{e}^{-q(T-0.2)}+0.91 \quad(0.2\;{\rm s}{\text{＜}}T{\text{＜}}4\;{\rm s}) $$ (4) 式中：T为结构自振周期；L为设防烈度；q为设防烈度影响系数，按照表6取值。
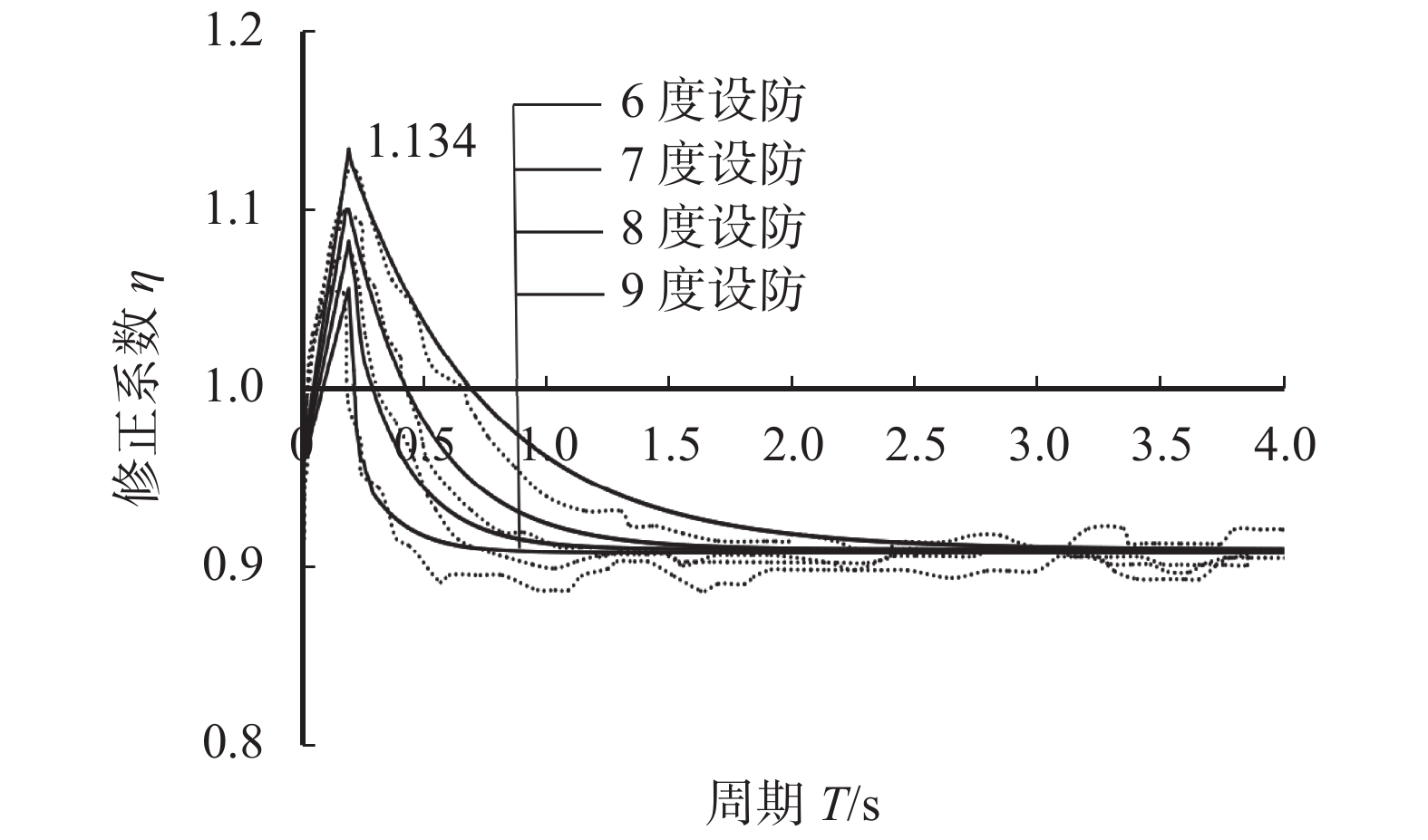
表 6 设防烈度影响系数q的取值Table 6. Value of the impact coefficient q of fortification intensity设防烈度L 6 7 8 9 q 1.8 3.2 4.6 6 图6为不同设防烈度下，根据上式绘制的修正系数曲线的拟合值与实际值的比较。图中黑实线为各级设防烈度下的修正系数拟合曲线，虚线代表对应的实际曲线。
图6可看出，拟合曲线能够很好地反映修正系数平均曲线变化趋势。
3 建立变阻尼比地震影响系数曲线
根据《建筑抗震设计规范》(GB50011—2010)的规定，可以用α表示地震系数k和动力系数
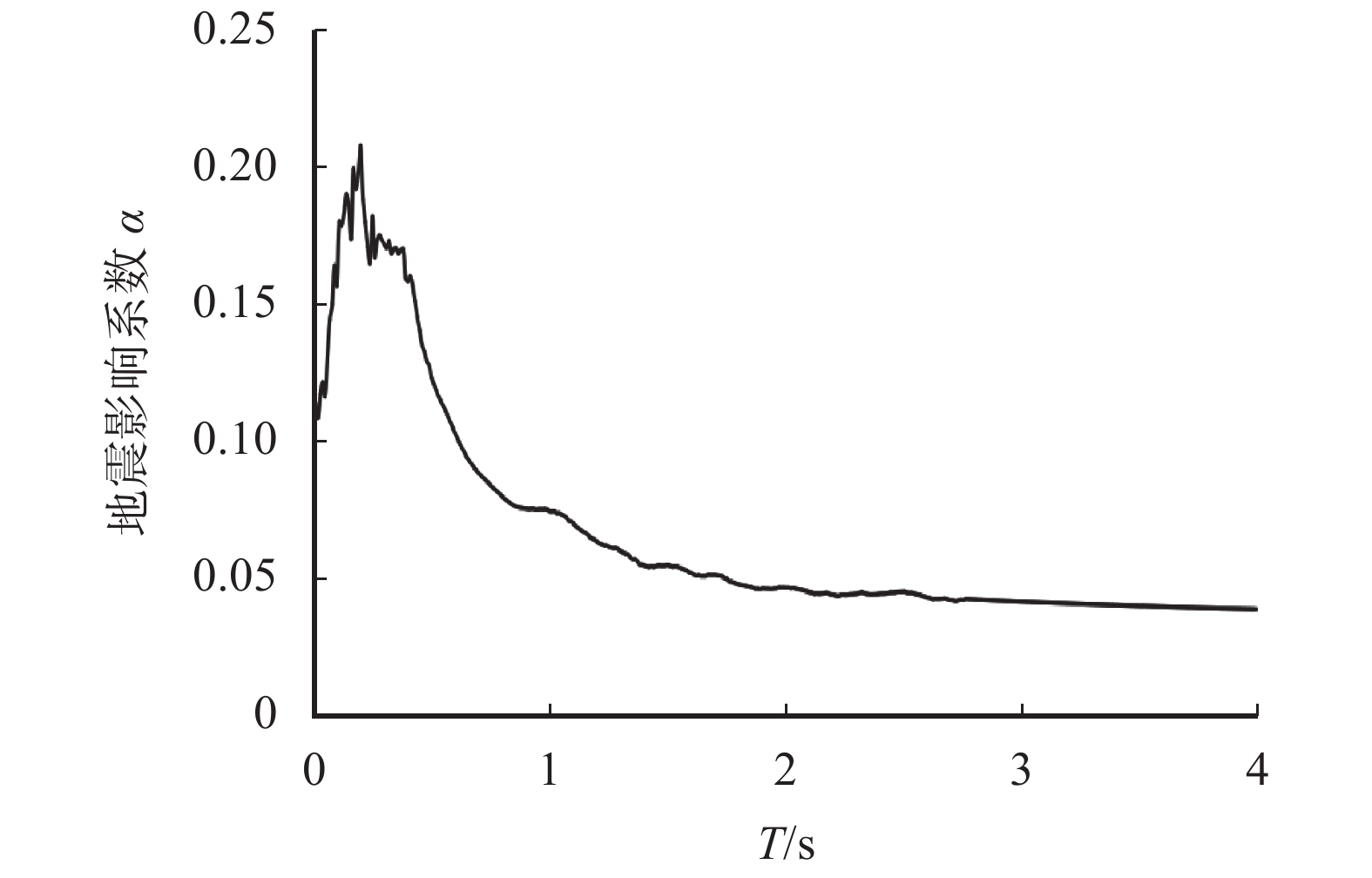
$ \beta $ 的乘积，并将该结果称为地震影响系数即：.$$ \alpha =k\beta {\text。} $$ (5) 根据图3得到的7度设防条件下的β谱和设防烈度下对应的地震系数k，可以得到对应的一条水平地震影响系数α曲线（图7）。
![]()
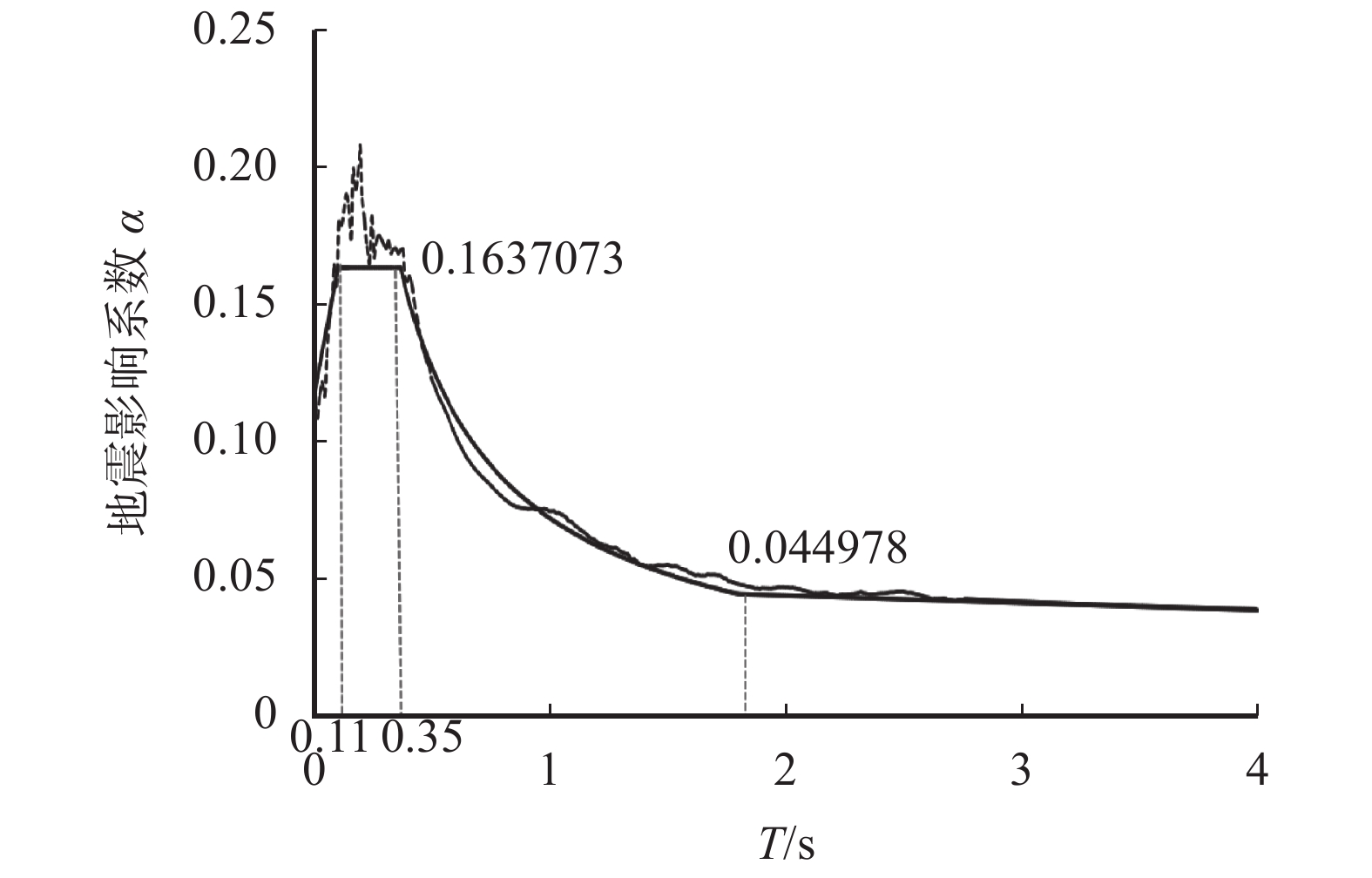
图 7 8 度设防水平地震影响系数曲线Figure 7. Seismic influence coefficient curve at 8 degrees fortification level将图7的水平地震影响系数曲线进行标准化处理，即将地震影响系数曲线变为标准化的平滑曲线，标准化后的影响系数曲线消除了在不同地震动强度下的差异性变化（图8）。
![]()
图 8 8 度设防水平地震影响系数规准曲线Figure 8. Seismic influence coefficient calibration curve at 8 degrees fortification level4 变阻尼比反应谱特性分析
影响地铁车站的地震响应有许多因素，如地震设防烈度、地震波的峰值和频率特性、场地条件以及结构埋深等。
4.1 地震设防烈度的影响
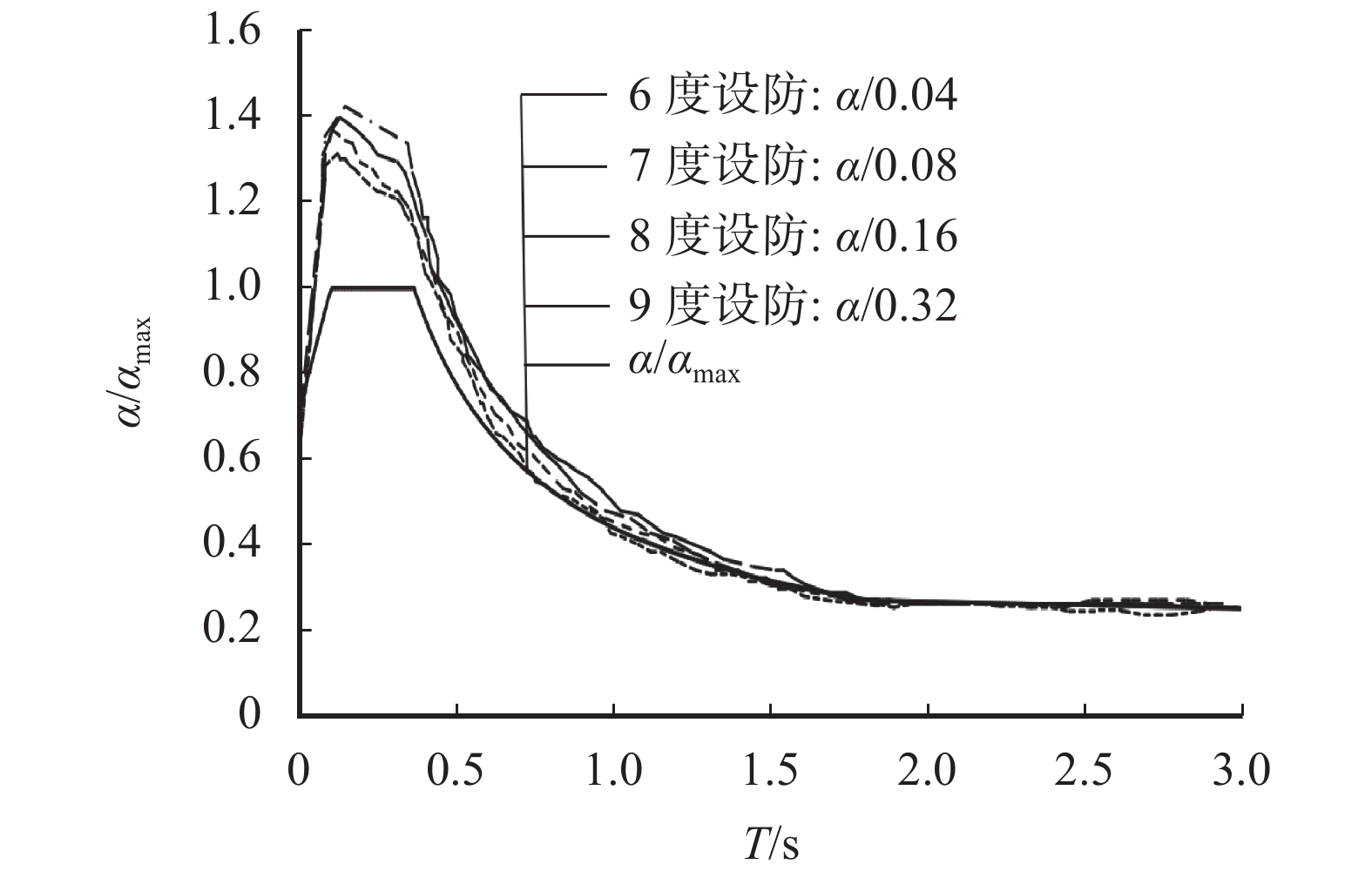
图9为不同设防烈度下的变阻尼比相对反应谱曲线。
![]()
图 9 不同设防烈度下的相对反应谱曲线Figure 9. Relative response spectrum curves of different fortification intensities从图9可以看出，不同设防烈度下的非线性阻尼比设计反应谱具有不同的形状，设防烈度越高，规准化反应谱越低，这与实际地下建筑结构的非线性阻尼机理相一致。由于此时结构变形较大，结构平均阻尼比超过5%，导致地铁车站结构规准化反应谱曲线中长周期部分在规准化标准反应谱线下方。
4.2 围岩参数的影响
围岩参数中影响反应谱(地震影响系数)的主要因素有：内摩擦角和黏聚力。由于现在既有明挖地铁车站多修建于浅埋土质围岩中，岩石围岩明挖车站比较少见。因此，主要针对Ⅴ、Ⅵ级围岩，不断改变内摩擦角和黏聚力得到不同参数条件下的反应谱，从而定量地给出两参数与地震影响系数的关系。基本围岩参数表如表7所示。
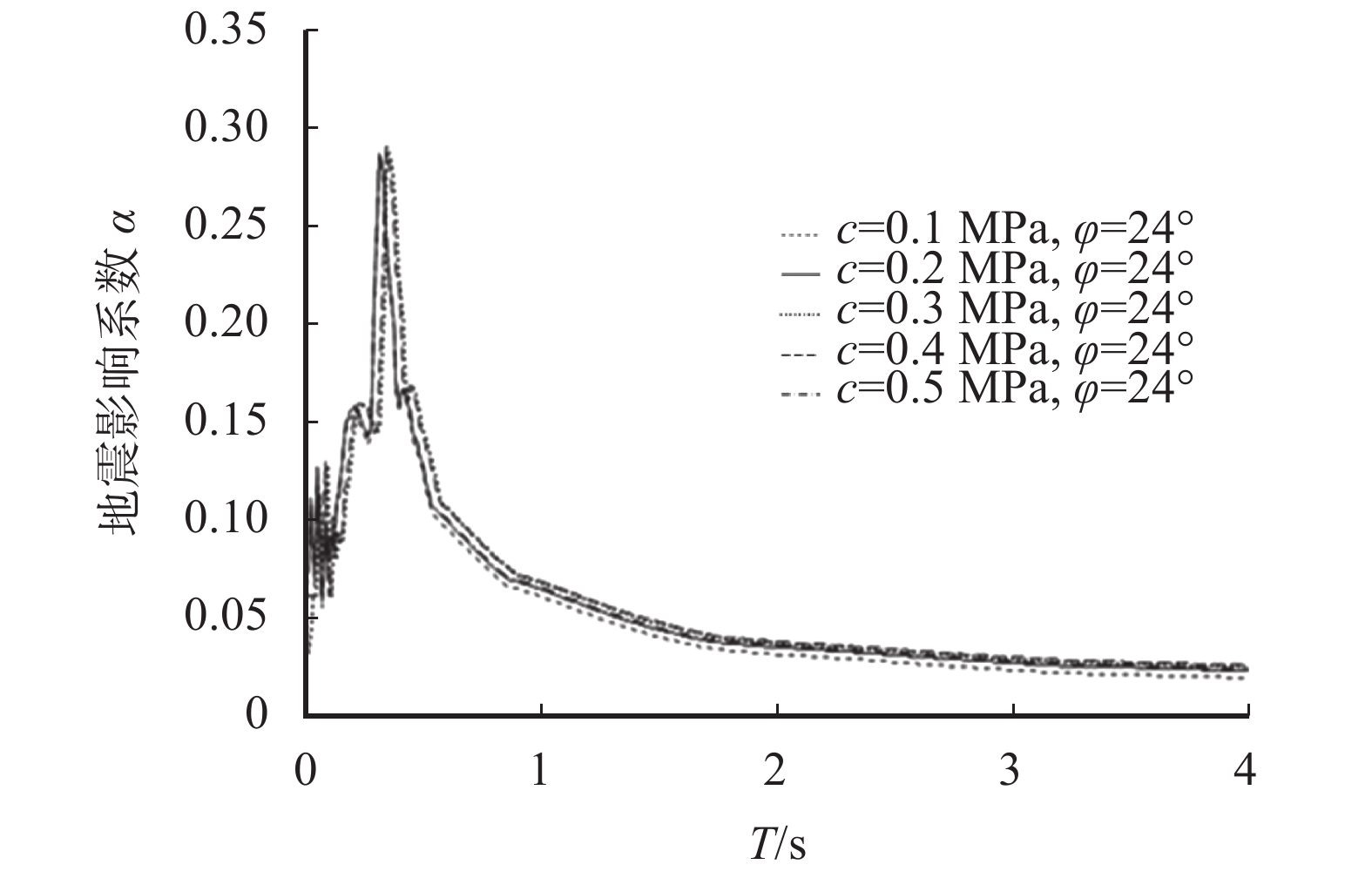
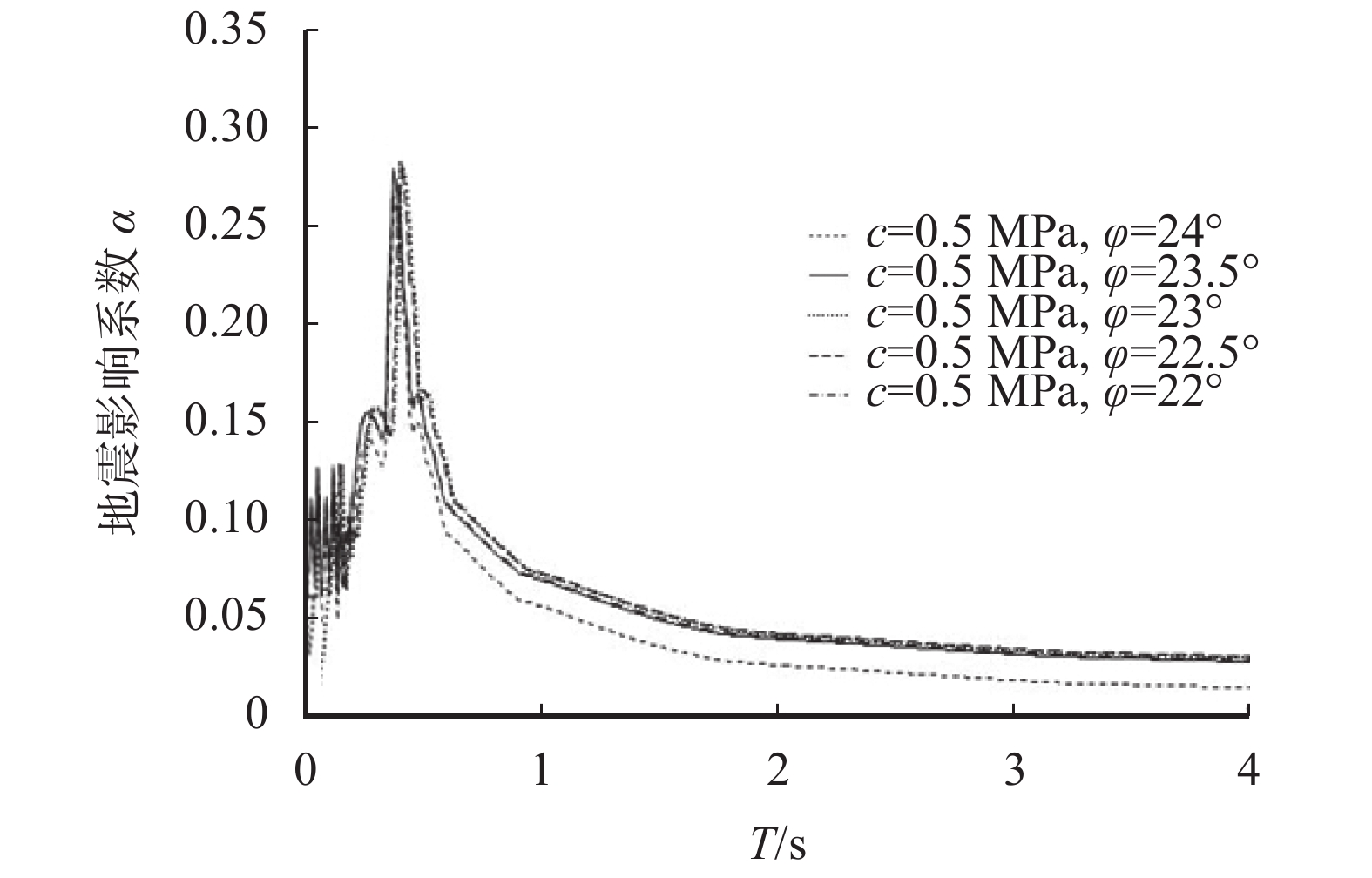
表 7 围岩材料力学参数Table 7. Mechanical parameters of surrounding rock materials围岩级别 弹性模量/GPa 泊松比ν 黏聚力/MPa 内摩擦角/(°) Ⅴ 1.5 0.4 0.125 23.5 Ⅵ ＜1 0.5 ＜0.1 ＜22 根据表7参数，运用控制变量法分别改变黏聚力、摩擦角以及泊松比，得到不同泊松比、黏聚力以及内摩擦角影响系数曲线（图10～12）。
![]()
图 12 不同内摩擦角影响系数曲线Figure 12. Influence coefficient curves of different internal friction由图10～12可知，黏聚力与内摩擦角的变化几乎没有引起反应谱的变化，只是在小范围内峰值发生了移动，移动量在0.01 s范围内；而当泊松比发生变化时，地震影响系数峰值及形状都发生了改变，峰值随泊松比的增大而增大，这就意味着围岩逐渐变弱时，地震对结构的影响在增大，地震影响系数当然要随之增大，但影响在数值和公式上的表示，还需要进一步探讨。
用同样的方法，使泊松比改变幅值尽量的小，每0.1划分为10份即增加幅值为0.01，定量地找出泊松比与地震影响系数峰值之间的对应关系。表8为由于泊松比的改变引起的地震影响系数峰值改变的规律。
表 8 泊松比与地震影响系数峰值关系Table 8. Relationship between Poisson's ratio and peak value of seismic impact coefficientν αmax ν αmax ν αmax 0.10 0.16 0.20 0.203 0.30 0.259 0.11 0.164 0.21 0.205 0.31 0.268 0.12 0.167 0.22 0.209 0.32 0.274 0.13 0.172 0.23 0.215 0.33 0.286 0.14 0.179 0.24 0.219 0.34 0.291 0.15 0.182 0.25 0.226 0.35 0.298 0.16 0.189 0.26 0.229 0.36 0.301 0.17 0.192 0.27 0.236 0.37 0.316 0.18 0.195 0.28 0.239 0.38 0.324 0.19 0.199 0.29 0.245 0.39 0.33 4.3 地下车站结构埋深的影响
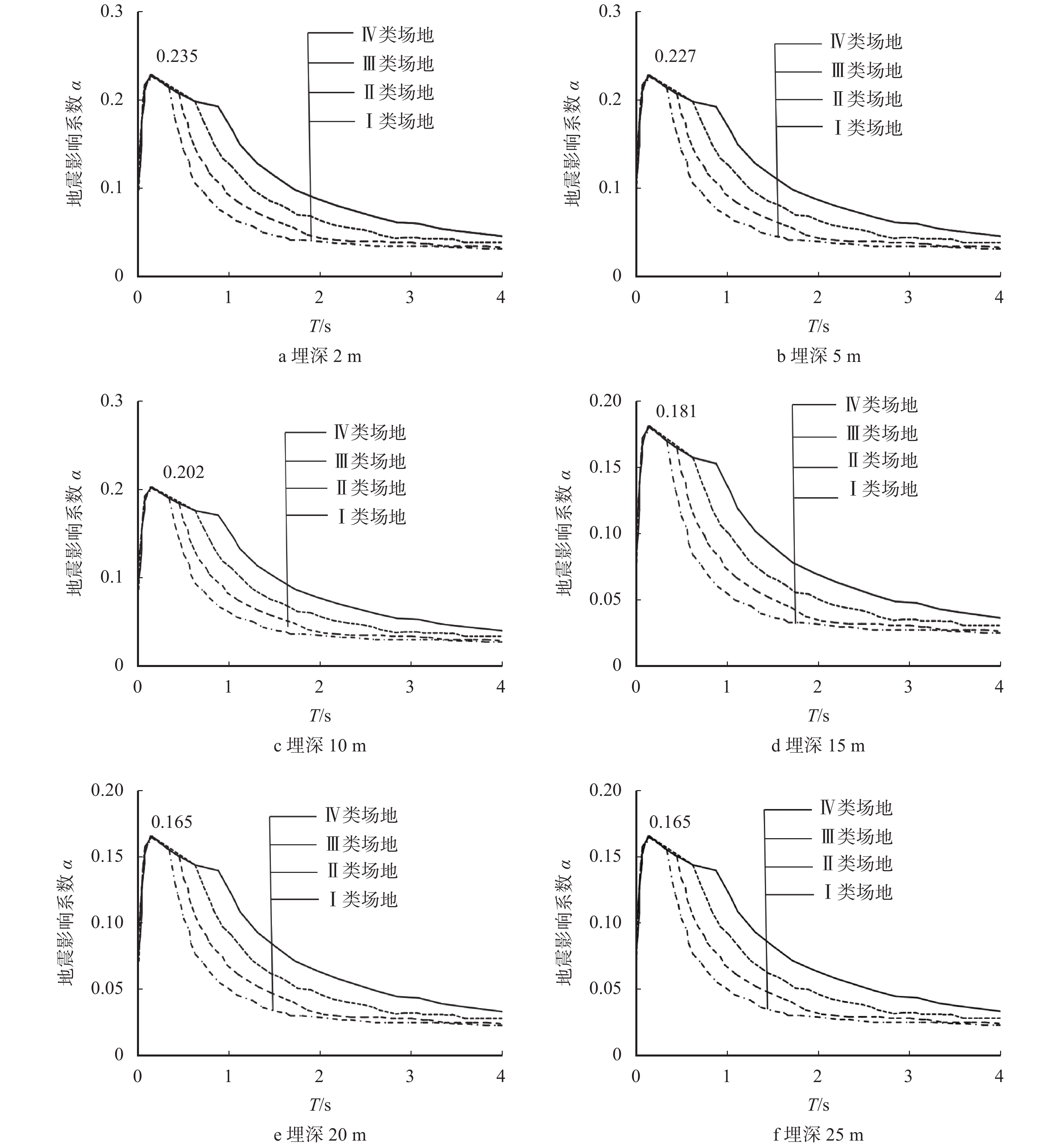
对埋深为2 m、5 m、10 m、15 m、20 m和25 m六种工况进行计算，进行平均规准化后得到各结果（图13）。
![]()
图 13 埋深对非线性阻尼比反应谱的影响Figure 13. Effect of burial depth on nonlinear damping ratio response spectrum由图13可以看出：随着埋深的增加，各类场地土的影响系数峰值逐渐减小。这是由于埋深的增大，在一种波的作用下有更多的土体对地震波起到了滤波作用，使得地震波加速度逐渐得到衰减，对地下结构的动力反应而言即逐渐减小；在埋深为2 m时更接近规准化设计反应谱的峰值，值为0.229。
5 结论
通过对单层双跨结构地铁车站进行动力数值模拟分析，研究各种因素下变阻尼比对反应谱的影响规律，并且在变阻尼比条件下对阻尼修正系数进行研究，得到如下结论。
1）不同设防烈度下的变阻尼比设计反应谱具有不同的形状，设防烈度越高，规准化反应谱越低，这与实际地下建筑结构的变阻尼机理相一致。
2）围岩参数中，黏聚力与内摩擦角的变化对结构的地震影响系数的影响较小，即只在小范围内峰值发生了移动；而当泊松比发生变化时，地震影响系数峰值及形状均明显发生了改变，峰值从泊松比为0.2时的0.17增加到了泊松比为0.4时的0.32，增大幅值近一倍。这就意味着围岩逐渐变弱时，地震对结构的影响在增大，地震影响系数当然要随之增大，
3）随着埋深的增加，在地震波的作用下，土体的滤波作用愈加明显，该作用加速了地震波能量的衰减，进而造成地下结构的动力反应程度较弱。当框架结构车站的埋深为2 m时，框架结构的反应谱峰值更接近规准化设计反应谱的峰值，值为0.229。
-
![]()
图 1 单层双跨车站横断面图(单位：mm)
Figure 1. Cross-sectional view of single-storey double-span station (mm)
![]()
图 4 地铁车站的变阻尼修正系数曲线
Figure 4. Variable damping correction coefficient curve of subway station
![]()
图 5 各设防烈度下变阻尼比修正系数曲线
Figure 5. Correction coefficient curves of variable damping ratio under different fortification intensities
![]()
图 7 8 度设防水平地震影响系数曲线
Figure 7. Seismic influence coefficient curve at 8 degrees fortification level
![]()
图 8 8 度设防水平地震影响系数规准曲线
Figure 8. Seismic influence coefficient calibration curve at 8 degrees fortification level
![]()
图 9 不同设防烈度下的相对反应谱曲线
Figure 9. Relative response spectrum curves of different fortification intensities
![]()
图 12 不同内摩擦角影响系数曲线
Figure 12. Influence coefficient curves of different internal friction
![]()
图 13 埋深对非线性阻尼比反应谱的影响
Figure 13. Effect of burial depth on nonlinear damping ratio response spectrum
表 1 分析结构的动力特性参数
Table 1 Analysis of dynamic characteristic parameters of structures
自振频率ω/(rad·s−1) 质量m/kg 刚度/(kN·m−1) 阻尼比ξ 93 2.79×106 9×105 0.05 
下载: 导出CSV
表 2 北京地区场地土模型物理力学参数
Table 2 Physical and mechanical parameters of site soil model in Beijing area
土性 厚度/
m密度/
(g·m−3)体积模量/
MPa剪切模量/
MPa黏聚力/
kPa内摩擦/
(°)填土 1 1.9 101.11 38 5 15 砂土 4.1 1.9 92.89 38 2 25 砂土 3.2 1.9 136.96 56 2 28 粘土 3.1 1.9 326.62 70 18 20 粘土 2.8 1.9 241.95 111.67 20 22 砂土 5 2.0 388.92 222.24 2 38
下载: 导出CSV
表 3 接触单元力学参数
Table 3 Mechanical parameters of contact elements
最大单元尺寸/
m法向刚度/
(Pa·m−1)切向刚度/
(Pa·m−1)黏聚力/
Pa内摩擦/
(°)0.6 1×108 1×108 0 5
下载: 导出CSV
表 4 选取地震波记录信息汇总
Table 4 Select seismic wave record information summary
编号 地震波 峰值/gal 持时/s 震级 震源深度/km 1 Friuli 0.35 36 6.5 9 2 Hollister 0.19 36 5.5 7.5 3 Imperial Valley 0.31 39 6.4 8.4 4 Kobe 0.33 41 6.9 11 5 Kocaeli 0.34 35 7.4 7 6 EL-centro 0.348 56 6.9 16 7 Trinidad 0.136 21 7 20 8 汶川波 约1 ＞120 8 19
下载: 导出CSV
表 5 结构相对剪切变形与阻尼比对照表
Table 5 Comparison table of relative shear deformation and damping ratio of structures
地震波编号 剪切应变(×10−3) 阻尼比 1 2.1 0.178 2 2.5 0.21 3 2.81 0.234 4 2.32 0.195 5 2.34 0.197 6 3.02 0.251 7 3.25 0.27 8 3.61 0.298
下载: 导出CSV
表 6 设防烈度影响系数q的取值
Table 6 Value of the impact coefficient q of fortification intensity
设防烈度L 6 7 8 9 q 1.8 3.2 4.6 6
下载: 导出CSV
表 7 围岩材料力学参数
Table 7 Mechanical parameters of surrounding rock materials
围岩级别 弹性模量/GPa 泊松比ν 黏聚力/MPa 内摩擦角/(°) Ⅴ 1.5 0.4 0.125 23.5 Ⅵ ＜1 0.5 ＜0.1 ＜22
下载: 导出CSV
表 8 泊松比与地震影响系数峰值关系
Table 8 Relationship between Poisson's ratio and peak value of seismic impact coefficient
ν αmax ν αmax ν αmax 0.10 0.16 0.20 0.203 0.30 0.259 0.11 0.164 0.21 0.205 0.31 0.268 0.12 0.167 0.22 0.209 0.32 0.274 0.13 0.172 0.23 0.215 0.33 0.286 0.14 0.179 0.24 0.219 0.34 0.291 0.15 0.182 0.25 0.226 0.35 0.298 0.16 0.189 0.26 0.229 0.36 0.301 0.17 0.192 0.27 0.236 0.37 0.316 0.18 0.195 0.28 0.239 0.38 0.324 0.19 0.199 0.29 0.245 0.39 0.33
下载: 导出CSV
-
[1] 王亚勇. GB 50011—2010《建筑抗震设计规范》和GB 18306—2015《地震动参数区划图》反应谱对比及地震动峰值加速度应用研究[J]. 建筑结构学报, 2020, 41(2): 1-6. [2] 张椿民. 地下多层地铁车站结构抗震设计对比分析[J]. 市政技术, 2022, 40(12): 50-58. [3] 李春锋, 张旸, 赵金宝, 等. 台湾集集大地震及其余震的长周期地震动特性[J]. 地震学报, 2006, 28(4): 417-428. [4] 袁勇, 杨澄宇, 蔡雪松. 基于模态等效法的地铁车站抗震虚拟实时混合试验研究[J]. 城市轨道交通研究, 2022, 25(8): 187-190,197. [5] 杨小礼, 王作伟. 非线性破坏准则下浅埋隧道围岩压力的极限分析[J]. 中南大学学报:自然科学版, 2010, 41(1): 299-302. [6] 李岩龙. 砂卵石地层不同结构型式大跨无柱地铁车站的抗震动力响应分析[J]. 城市轨道交通研究, 2021, 24(3): 107-111. [7] 齐明山, 蔡晓鸿, 冯翠霞. 隧道围岩压力的弹塑性新解[J]. 土工基础, 2006, 20(2): 73-76. [8] 朱雯蕾, 李宁. 青岛地铁某地下车站结构抗震数值模拟计算分析[J]. 现代城市轨道交通, 2020(1): 65-72. [9] 夏栋舟. 土—结构动力相互作用(SSDI)体系阻尼性能及其地震反应分析与研究[D]. 长沙: 湖南大学, 2009. [10] 毕继红, 张鸿, 邓芃. 基于耦合分析法的地铁隧道抗震研究[J]. 岩土力学, 2003, 24(5): 800-803. doi: 10.3969/j.issn.1000-7598.2003.05.025 [11] 梁剑. 地铁地下结构抗震分析及设计中的关键问题[J]. 建筑技术开发, 2017, 44(11): 21.
计量
- 文章访问数: 202
- HTML全文浏览量: 52
- PDF下载量: 50
